SAHIWAL BOARD 2015
INTER
PART-II
Mathematics
(Session: 2015)
Time: 20Minutes
(OBJECTIVE)
Marks: 20
Note: - Write answers to the questions on objective answer sheet provided, four possible answers A, B, C & D to each question are given. Which answer you consider correct, fill the corresponding circle A, B, C or D given in front of each question with Marker or pen ink on the answer sheet provided.
- Co-vertices of the ellipse 4 9 -+ -1 are:
- (±2, 0)
- (±3, 0)
- (0, ±3)
- (0, ±2)
- Work done by a force F during displacement d equals
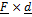
-
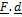
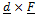
-
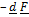
- Focus of parabola x2: 16y equals
- (0,4)
- (0,-4)
- (0,16)
- (0,-16)
- Te radius of circle x2+ y2+ 6o + 8y + 9 r. 0
- 6
- 8
- 9
- 4
- Solution set of Inequality 2x – 3
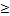 0 equals
0 equals

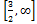
-
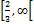
-

- Length of perpendicular from (0,0) to line 4x-3y-1=0 equal
- 3
- 4
- 5

- If two lines with slopes m1 and m2 and m2 are parallel , then
- m1.m2=1
- m1.m2=-1
- m1-m2=0
- m1+m2=1
 equals
equals
- ex/x
- ex.ln x
- xex
- x.ln x
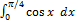 equals
equals
- 1
- 2
-

-
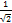
 dx is equal to
dx is equal to
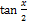

-
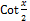
-
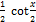
 dx equal
dx equal
- tan-1x
- tanx-2
- cot-1x-2
- cot-1x
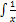 is equal to
is equal to
- Ln
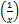
- ln x
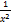
-
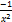
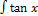 dx equals
dx equals
- ln sec x
- ln cos x
- ln sin x
- -ln sin x
- Derivation of ln(1-cos x ) w.r.t. x equals
- tan x
- tan x/2
- cot x/2
- cot x
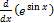 equals
equals
- esinx.cos x
- -esinx.cos x
- ecosx.sin x
- -ecosx.sin x
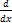 (sin 2x) is equal to
(sin 2x) is equal to
- cos2x
- 2cos2x
-
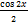
-
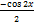
- Derivative of sec-1 x equals
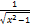
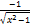

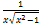
 (cosh x) is equal to:
(cosh x) is equal to:
- Sin h x
- -sin h x
- cosh x
- -cosh x
- If f(x) =2x-1, then f-1 (x) equals
- 1-x
- 1+x
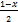
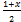
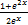 is equal to
is equal to
- sinh x
- –sinh
- cosh x
- -cosh x
SAHIWAL BOARD2015
Mathematics
(Session: 2015)
Time: 2:10Hours
(SUBJECTIVE)
Marks: 80
Note: Section I is compulsory. Attempt any three questions from Section II and any Two parts from Section III.
SECTION-I
2. Write short answers to any Eight questions.
- Prove the identity sin h 2x = 2sin h x cos h
- Evaluate:
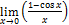
- Express in terms of e,
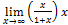
- Find
 by definition if
by definition if 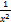
- Differentiate: w.r.t x

- Differentiate: (1 + x2)n w,r.t x2.
- Differentiate: sin3x w.r.t cos2x
- Find
 if y x=cos y
if y x=cos y
- Find
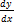 if y =
if y =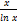
- Find y2 if y = x2e-x
- By Maclaurin's series prove that e2x= 1 + 2x +
 + ……..
+ ……..
- Find the interval in which f is increasing or decreasing, f (x) = sin x ; x
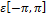
3. Write short answers to any Eight questions.
- Using differential find
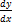 in the ay - In x = c
in the ay - In x = c
- Using differentials to approximate the value of
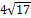
- Evaluate:
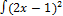
- Evaluate:
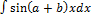
- Evaluate:
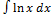
- Evaluate
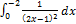
- Evaluate

- Find the area between the x-axis and the curve, y = 4x-x2
- Evaluate :
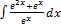
- Solve the differential equation xdy+y(x-1)dx=0
- Graph the solution set 3y - 4
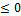 in xy - plane.
in xy - plane.
- What is an objective function?
4. Write short answers to any Nine questions.
- Show that the points A (0,2), B (
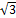 ,-1) and C (0,-2) are vertices of a right triangle
,-1) and C (0,-2) are vertices of a right triangle
- Find the points trisecting the join of A (-1, 4) and B (6,2).
- Find slope and angle of inclination of line joining the points (4,6) and (4,8).
- Find equation of line through the point (2, -9) and the intersection of the
- lines 2x + 5y-8= 0 and 3x- 4y- 6 = 0
- Vertices of triangle are A (-2, 3), B)-4, 1) and C (3,5). Find coordinates of centroid.
- Find centre and radius of circle x2 + y2- 6x + 4y + 13 = 0
- Write equations of tangents from (2, 3) to the circle x2+ y2=9
- Find focus and directrix of parabola y2 = 8x
- Find centre, foci and eccentricity of the ellipse x2 + 4y2= 16
- Find a unit vector in the direction
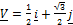
- Find a so that
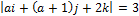
- If
 -
-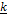 , =
, =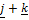 .Find projection of a along b.
.Find projection of a along b.
- If
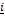 -2
-2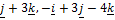 and
and 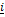 -3
-3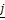 +5
+5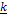 are coplanar
are coplanar
SECTION-III
Q.5.
(a) Define continuous function Discuss the continuity of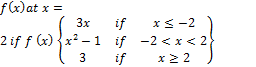
(b) Find the derivative of 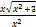 with respect to x
with respect to x
Q.6.
(a) Evaluate: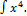 ln x dx
ln x dx
(b) By means of slopes, show that the points lie on the same line (-1, -3) , (1,5) ,(2,9)
Q.7.
(a) Evaluate: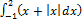
(b) Graph the feasible region of the following system of linear inequalities and find and the corner points.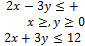
Q.8.
(a) Find the equation of the circle that passes through the points A(4,5), B(-4,-3), C(8,-3)
(b) Using vector method prove that in any triangle ABC c = a cos B + b cos A
Q.9.
(a) Find equation of the parabola having its focus at the origin and directrix parallel to the y - axis.
(b) Find volume of the tetrahedron with the vertices (0,1,2); (3,2,1), (1,2,1) and (5,5,61)
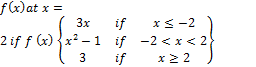
![]() with respect to x
with respect to x![]() ln x dx
ln x dx ![]()
![]()