SAHIWAL BOARD 2015
PAPER STATISTICS
PART-II
Time: 20
(Objective Part)
Note: Four Answers are given against each column A,B,C&D. Select the write answer and only separet answer sheet, fill the circle A,B,C or D with r a or marker in front of that question number.

Question#1

• Power of test is denoted by:
  
  (a) α
  (b) 1-α
  (c) β 
  (d)1-β
  
  
• A hypothesis which is to be tested for possible rejection is called hypothesis.
  
  (a) Null 
  (b) Alternative
  (c) Composite
  (d) Simple
  
  
• In simple linear regression equation, the number of independent variables is.
  
  (a) 0
  (b) 1
  (c) 2
  (d) 3
  
  
• If cov(x,y) = 0 then coefficient of correlation is:
  
  (a) Negative
  (b) Positive
  (c) Zero                                          
  (d) None of these
  
  
• Correlation coefficient lies between.
  
  (a) 0 and +1
  (b) -1 and +1
  (c) -1 and 0
  (d) Only 1
  
  
• Coefficient of association (Q) ties between.
  
  (a) 0 and + 1
  (b) -1  and +1
  (c) -∞ and 1
  (d) -1 and + ∞
  
  
• If (AB) < 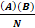 then association will be:
  
  (a) Zero  
  (b) Negative
  (c) Positive
  (d) Symmetrical
  
  
• Graph of time series is called:
  
  (a) Histogram
  (b) Historigram
  (c) Ogive                                            
  (d) Pie-chart
  
  
• Systematic component of time series which follow regular pattern is called:
  
  (a) Model
  (b) Random
  (c) Noise                                                  
  (d) Signal
  
  
• 1024 MB is equal to:
  
  (a) 1 KB 
  (b) 1 GB  
  (c) 1 MB 
  (d) 1 Byte
  
  
• Area under normal curve on either side of mean is:
  
  (a) 1
  (b) 0.5
  (c) 2 
  (d) 1.5
  
  
• Normal distribution is:
  
  (a) Leptokurtic                            
  (b) Platykurtic
  (c) Mesokurtic                                        
  (d) None of these
  
  
• In normal distribution is always:
  
  (a) < 0 
  (b) > 0 
  (c) 3
  (d) = 0
  
  
• In sampling without replacement:
  
  (a) n <N                                   
  (b) n = N             
  (c) n > N
  (d) None of these
  
  
• In sampling without replacement, a sampling unit can be selected.
  
  (a) Once                                
  (b) Twice
  (c) Less than once                              
  (d) More than once
  
  
• Sum of frequencies of sampling distribution is equal to:
  
  (a) Population size
  (b) Sample size
  (c) Possible samples
  (d) None of these
  
  
• Level of confidence is denoted by:
  
  (a) a 
  (b) 1-a
  (c)  β
  (d) 1-β

Time: 2:40 Hours 
(Subjective Part)
Marks: 68
SECTION-I

2. Write short answers of any Eight Parts. 16

1. Define normal probability distribution.
   
2. What is the role of σ in normal distribution?
   
3. Define the normal cumulative distribution function.
   
4. Find maximum ordinate of normal curve if σ=4.
   
5. If X ̴ N (24, 16). Find Q1 and Q3.
   
6. What is meant by statistical inference?
   
7. Define the term biased estimator.
   
8. Define the term Null Hypothesis.
   
9. What is two-tailed test?
   
10. What is hybrid computer?
    
11. What is CPU?

3. Write short answers of any Eight Parts. 16

1. Give any two advantages of sampling.
   
2. Define parameter and statistics.
   
3. Define non sampling error and sampling error.
   
4. Given that µ=50.σ2=250 find µ
5. , α2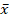 if sampling is done with replacement for n = 50.
   
6. Write the formula of biased and unbiased variance.
   
7. Define sampling distribution and standard error.
   
8. Define the term correlation and regression.
   
9. Write any two properties of correlation co-efficient.
   
10. Define the principles of least squares.
    
11. What is meant by dependent variable?
    
12. What is meant by independent variable?
    
13. Write any two properties of least square line.

4. Write short answers of any Six Parts. 12

1. When two attributes are said to be associated positively?
   
2. Given that (AB)=30,(A)= 40 , Find (Aβ)= ?
   
3. Define rank correlation.
   
4. Define a time series.
   
5. Explain with examples the secular trend.
   
6. Write multiplicative model of the time series.
   
7. Define signal.
   
8. A straight line is fitted to a time series y= 210 + 2 x to the years1995.1999) taking origin at 1995, Find trend values.
   
9. Given y = 132 + 2.4 x is fitted to the year (2004-2008) with origin at 2006. Find estimated value for the year = 2010.

SECTION II

Attempt any THREE Questions. Each Question carries 8 marks.
Question#5
(a) If mean of the normal distribution is 100 and S.D is 20, then find 04
(i) Area between 65 and 85
(ii) Area below 85
(iii) Area between 65 and 125
(b) In a normal distribution µ =30 and σ =5, what proportion of cases will fall between 20
and 35.  04

Question#6
(a) If the size of the simple random sample from an infinite population is 36 and standard error of mean is 2. What must be the size of sample becomes if the standard error is to be reduced to 1.2. 04
(b) Given a population. X = 3, 4, 5. Select all possible samples of size 2 with replacement from this population and verify that: 04
(i) µx =µ 
(ii) σ2:=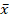  

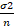
Question#7
(a) Find a 95% confidence interval for "P" if 24 heads are obtained in 40 tosses of a coin.04
(b) Let X ̴ N (µ,100) and 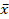 be the mean of a random sample of 64 observations of x, given that 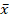=15. Test Ho: µ=12 against the alternative H1 = µ >12. Use a 0.05. 04

Question#8
(a) The following statistics have been computed. 04
= 14.9,y=21.65,Sx=5.71,Sy=6.73,r = 0.651, Construct the two regression equations.
(b) The equations of two regression lines y on x and x only respectively are given from paired observations of two variable x and y : 8x – l0y + 66 = 0 and 40x - 18y - 214 = 0.Compute and interpret the coefficient of correlation.04

Question#9
(a) Given that (A)=(a)=(B)=(β)= n/2 show that
(i) (AB). (aβ)
(ii) (Aβ). (αB) ,
(b) Compute the trend values by 3-year moving average method from the following time series. 04

SECTION-III
(Practical Part)

10. Attempt any THREE questions.
(A) Make all possible samples of size 2 with replacement from the population 8, 16, 24. From sampling distribution of sample means and verify that var (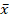) =         05
(B) Two random samples taken independently from normal population yielded the followings results. Test the hypothesis that the true difference between the population mean is at most 10.

(C) Compute the Correlation coefficient 05

(D) Test the association between the subject and results from the following, data: 05

(E) Find the trend values by the method of least square.