(A)![]() -
-![]()
(B) ![]() +
+![]()
(C) ![]() -
-![]()
(D)![]() +
+![]()
Sargodha Board
( Inter Part- II)
(Session 2015)
Mathematics
(Objective)
Paper (1)
Time Allowed:- 30 minutes
Maximum Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles will. Cutting or filling two or more circles will result in zero mark in that question. Write PAPER CODE, which is printed on this question paper, on the both sides of the Answer Sheet and fill bubbles accordingly, otherwise the student will be responsible for the situation. Use of Ink Remover or white correcting fluid is not allowed
(A)
-

(B)+
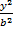
(C)-
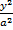
(D)+
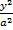
(A)1
(B) •1
(C) 0
(D) 2
(A) e-x
(B) ex
(C) xex
(D) xex-1
(A) Sec2x
(B)-Sec2x
(C) Cosec2x
(D) - Cosec2x
(A) Cosh 2x
(B) Sinh 2x
(C)2Cosh 2x
(D) 2Sinh 2x
(A) -

(B)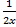
(C)
(D)
(A)sin 2x
(B) cos 2x
(C) –sin 2x
(D)-cos 2x
(B)
(C)
(D)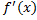
(A)–Sinx
(B) –Cosx
(C)Sinx
(D) Cosx
(A)ex+1
(B)ex-1
(C)e1-x
(D) ex
(A)
(tan-1+ x)
(B)(Cot-1x
(C)(tan-1+ x2)
(D)(Cot-1x2)
(A) 3/10
(B)
(C) 2
(D)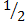
(A)
(B)
(C)
(D) 0
(A) h2-ab=0
(B) h2+ab = 0
(C) a + = 0
(D) a -b= 0
(A) (
, -2)
(B) (, 2)
(C) (2,)
(D) (-2,)
(A) Constraints
(B) Variables
(C) Decision Variable
(D) Vertices
(A) y = ±
(B) x= ±
(C) y = ±
(D) x = ±
(A) (-1 , -3)
(B) (1, 2)
(C) (1 , -2)
(D) (-1 2)
(A) ab Sinθ
(B) ab Sinθn
(C) ab Cosθ
(D) ab Cosθn
(A) 1
(3) 2
(C) 3
(D) 4
Mathematics (Subjective)
(Session 2015)Paper (1)
Time Allowed: 2.30 hours
(Inter Part -II) Group-I
Maximum Marks: 80
Section-I
2.Answer briefly any eight parts from the followings:
3. Answer briefly any Eight parts from the followings:
4. Answer briefly any Nine parts from the following
Section-2
Note: Attempt any three questions.
5.(a) Find values of m, n, so that the function f(x) is continuous at x = 3 where
f (x)=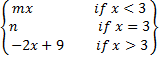
(b) Differentiaie y = Sin ![]() from the first principe
from the first principe
6.(a) Evaluate ![]() dx
dx
(b) Find joint-equation of line through (0.0) perpendicular to ax2+2hxy+by2=0
7.(a) Evaluate ![]()
(b) Maximize f(x,y)=2x+5y subject to the constraints;

8.(a) Find an equation of the circle passing through A (3,-1), B( 0,1)and having centre at 4x - 3y -3=0
(b) Prove by vector method that Cos (α + β)=CosαCosβ –Sinα Sinβ
9.(a) Find the equation of the ellipse when Foci (±3 , 0) and the minor axis of length 10
(b) Find the volume of the Tetrahidron with the vertices ( 0,1,2 ), ( 3 , 2 , 1 ) ( 1,2 ,1) , (5,5,6)