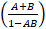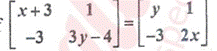FAISALABAD BOARD 2016
PAPER MATHEMATICS
PART-I
Time 30 Min.
(Objective Part)
Marks: 20
Note:   Four Answers are given against each column A,B,C& D. Select the write answer   and only separet answer sheet, fill the circle A,B,C or ,D with pen or marker in front of that question number.

Question#1

• cos x =  has solution:
  
  (a)                   
  (b)
  (c)                          
  (d)
  
  
• cos^-1(-x) = :
  
  (a) π – cos^-1
  (b) cos^-1 x
  (c)  - cos^-1 x
  (d) π + cos^-1
  
  
• If Δ is the area of a triangle ABC, then A = :
  
  (a)   ab sin γ
  (b)  ab sin β
  (c)  ab cos γ
  (d)  ab cos β
  
  
  
•    =:
  
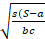  (a) sin    
  (b) sin
  (c) cos
  (d) cos
  
  
• The period of sin x is :
  
  (a) 0
  (b) π
  (c) 2π
  (d)
  
  
•    = :
  
  (a) sin Ɵ
  (b) cot
  (c) cos sec2 Ɵ
  (d) tan
  
  
• What is the vertex of the standard angle?
  
  (a)  (1,1)
  (b)  (0,1)
  (c)  (1,0)
  (d)  (0,0)
  
  
• If n is even, then middle term in expansion of (X+Y)n
  
  (a) th term                             
  (b) th term
  (c) 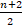th term                         
  (d) nth term
  
  
• Sum of bionomial coefficients is :
  
  (a) n
  (b) 2n
  (c) 2ⁿ
  (d) n²
  
  
• If a faor on coin is tossed, then probability of head appear:
  
  (a)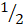
  (b) 2
  (c) 0
  (d) 1
  
  
• n P_r = :
  
  (a) ⁿ⁺¹ P_r
  (b) ^n-1 P_r
  (b) r!”P_r 
  (d) r!”C_r
  
  
• Arithmetic mean between x - 1 and x + 1 is equal to:
  
  (a) 0
  (b) 2
  (c) x                                        
  (d) 2x
  
  
• The next term of the sequence 1, 3, 6, 10,……is:
  
  (a) 13                                      
  (b) 15
  (c) 17
  (d) 19
  
  
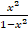•    is:
  
  (a) Proper fraction
  (b) Improper fraction
  (c) Equation
  (d) Decimel
  
  
• What is the value polnimial 3- 7x + 1 at x = -1 is :
  
  (a) -0
  (b) 3
  (c) 9
  (d) 11
  
  
• If A is a matrix of order 3 x 4 then order of AA' is:
  
  (a) 4 × 3
  (b) 3 × 4
  (c) 4 × 4
  (d) 3 × 3
  
  
• A function which is onto is called:
  
  (a) Injective
  (b) Surjective
  (c) Objective
  (d) Bijective
  
  
• 1- a + a2 = :
  
  (a) -1
  (b) 0
  (c) 1
  (d) 0
  
  
• A functional which is not is called:
  
  (a) -1
  (b) 1
  (c) I                                        
  (d) –i
• If the matrix 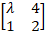 is singular, then λ = :
  
  (a) 2
  (b) 4
  (c) 1
  (d) 0

Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I

2.Attempt any Eight Parts.16

• Define rational numbers.
  
• Simplify: (8,-5) - (-7,4)
  
• ∀z∋C show that z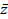=  |z|².
  
• Write the set {x |x∈Q 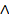x2 = 2} in tabular form.
  
• Show that (p 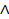 q)→p is a tautology.
  
• Let G be a group and a, b ∈ G Solve ax = b and xa = b.
  
  
• Find x and y if
  
  
  
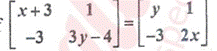
• Find inverse of
  
• If A and B are non singular matrices then show that = (AB)^-1 = B^-1 A^-1
  
• Discuss nature of roots of equation  x2 - 5x + 6 = 0
  
• Show that is factor of x -2 is factor of 13x2 + 36
  
• Solve 5x2- 2ax-a2 = 0 by quadratic formula.

3.Attempt any Eight Parts.16

• Define identity.
  
• How many terms of -7+ (-4) + (-1) + ……… amount to 114.
  
• Find vulgar fraction equivalent to 1.53.
  
• If  ,  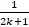,  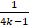are in H.P, find K.
• If  ,  ,  are in G.P., find r =±
  
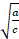
• Define sample space.
  
• Find , if  =ft C6.
  
• How many words can be formed from OBJECT using all letters?
• Prove that  ⁿC₁₂ =ⁿ C₆.
• Expand (8 – 2x)-1 upto two terms.
• Show that n!> n2 is true for n = 4,5 .
• Find the 6th term in the expansion of 
  (x-2/x)¹⁰

4. Attempt any Nine Parts.  18

• Prove that cos4Ɵ – sin4Ɵ = cos2Ɵ – sin4Ɵ
  
• Find x, if tang 45° - cos260° = x sin 45° cos 45° tan 60°
  
• Define radian.
  
• Find the distance between the points P(cos x,cos y) and Q (sin x, sin y)
  
• Without using tables / calculator, find the values of sin105° and cos105°.
  
• Prove that 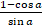 = tan  = tan
  
• Find the period of  3cos
  
• Solve the right triangle ABC in which y = 90°, β = 796 ,a = 62°40
  
• Find the smallest angle of triangle ABC when a = 37.34, b = 3.24, c = 35.06
  
• With usual notations, prove that R =  .
  
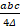• Without using tables / calculator, show that tan-1  = sin-1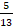
  
• Solve sin x + cos x = 0 where x ∈,2π]
  
• Solve 2 sin2Ɵ –sine Ɵ= 0 where Ɵ ∈ [0,2π]
  
  

SECTION-11

Attempt any THREE questions. Each questions carries 10 marks.
Question#5
(a) Use the cramer,s rule to solve the system
3xi + x2- x3 = -4
x, + x, — 2x3 = -4
-x, + 2x2 - x3 = 1
(b) Find the condition that one root of  ax2  + bx + c = 0 , a # 0 is square of the other.

Question#6
(a) Resolve into partial fractions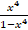
(b)        If the 5th term of an A.P. is 16 and the 20th term is 46, what is its 12th term?

Question#7
(a)Show that  n+1Cr + n+1Cr  = nCr
(b) Find the term independent of  x in the expansion of x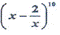

Question#8
(a) If cot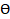=   and the terminal arm of the angle is in first quardrant, find the value of

(b) Prove tha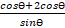t   = cot

Question#9
(a) Solve the triangle ABC, in which a = 36.21, c = 30.14, β = 78°10' by using first law of tangents and then law of
sines.
(b) Prove that tan -1 A + tan -1 B = tan -1