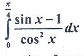FAISALABAD BOARD 2016
PAPER MATHEMATICS
PART-II
Time: 30 min
(Objective)
Marks: 20
Note:Four Answers are given against each column A,B,C&D. Select the write answer and only separate answer sheet, fill the circle A,B,C or with pen or marker in front of that question number.
Question#1
- 2
 ×
×  .
. =:
=:
(a) 2
(b) 0
(c) I
(d) -2
- For any two vectors
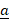 and
and 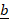 projection
projection 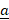 of
of 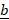 on b is:
on b is:
(a) 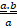
(b) 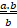
(c) 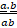
(d) 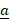 .
.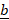
- Focus of the parabola y2 = -4ax is:
(a) (a, 0)
(b) (-a,0)
(c) (0,a )
(d) (0,-a)
- Center of the circle 5x2 + 5y2 + 14x + 12y -10 = 0 is at:
(a) (-7,-6)
(b) 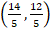
(c) (7,6)
(d) 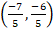
- Point (1, 2) lies in the solution region of the inequality:
(a) 2x + y > 5
(b) x + 3y > 5
(c) 2x + y < 3
(d) 2x + y > 6
- The distance of the line 12x + 5y = 7 from origin is:
(a) 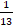
(b) 
(c) 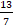
(d) 13
- If a = 0 then the line ax + by + c = 0 is:
(a) Parallel to x-axis
(b) Parallel to y-axis
(c) Perpendicular to x-axis
(d) Passes through origin
- Distance of (-3, 7) from x-axis is:
(a) -3
(b) 3
(c) 7
(d) 10
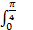 sec2 x dx =:
sec2 x dx =:
(a) I
(b) 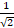
(c)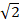
(d) 0
-
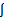
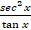 dx =:
dx =:
(a) tan x
(b) cot x
(c) ℓn cot x
(d) ℓn tan x
- ʃ cos sec2 2xdx =:
(a) cos 2x
(b) 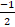 cot 2x
cot 2x
(c) 2 tan 2x
(d)  cot 2x
cot 2x
- ʃ
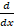 (xn) dx=:
(xn) dx=:
(a) 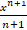
(b) Xn
(c) nxn-1
(d) xn-1
- ʃ tan x dx = :
(a) ℓn sec x
(b) sec2 x
(c) ℓn cos x
(d) in sin x
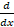 (
(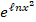 =:
=:
(a) 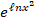
(b) 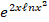
(c) 2x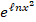
(d) 2x
- If ʃ’ (c)= 0 and ʃ n(c) < 0 then f (x) will give at x = c:
(a) Maximum value
(b) Minimum value
(c) Neither maximum nor minimum value
(d) Stationary value
-
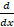
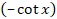 = :
= :
(a) –cos sec x cot x
(b) co sec x cot x
(c) cos sec2 x
(d) –cos sec2 x
- If ʃ (x) = 3 -
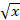 then ʃ (1) = :
then ʃ (1) = :
(a) 
(b) 
(c) 
(d) 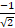
- The function f (x) = cos x + sin x is:
(a) Even
(b) Odd
(c) Neither even nor odd
(d) Both even and odd
- If f (x) = x sec x then f (0):
(a) -1
(b) 1
(c) 0
(d) ∞
Time: 2:30 Hours
(Subjective Part)
Marks: 80
SECTION-I
2. Attempt any Eight Parts. 16
- If f (x) = sin x + cos x . Check whether f is even or odd, neither f is even nor odd.
-
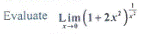
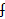 (x) =
(x) = 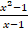 , check whether f is continuous or not continuous at x = 1
, check whether f is continuous or not continuous at x = 1- If y =
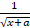 , find
, find 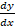 .
.
- Differentiate x2 sec4x w.r.t x.
- Differentiate ℓn (e2 + e-3) w.r.t. x.
- Differentiate ℓn
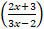 w.r.t x.
w.r.t x.
- Differentiate y = sinh-1 (x3) w.r.t x.
- Differentiate (ℓnx)2 w.r.t x.
- If x2 +y2 = a2 ,find
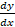
- Apply Maclaurin series to prove ex = 1+ x +
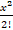 + ……
+ ……
- Differentiate (x+4
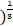 w.r.t x.
w.r.t x.
3. Attempt any Eight Parts. 16
- Using the differential find
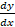 in the equation Ay + x = 4.
in the equation Ay + x = 4.
- Evaluate ʃ
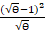 dƟ
dƟ
- Evaluate ʃ
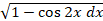 .
.
- Evaluate ʃ sin2 xdx .
- Evaluate ʃ tan2 xdx .
- Evaluate ʃ
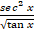 dx.
dx.
- Evaluate

- Evaluate

- Find the area between the x-axis and the curve y = sin2 x, from X = 0 to x =
 .
.
- Solve the differential equation
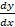 =
= 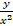 .
.
- What is an objective function?
- Graph the solution set of the linear inequality 5x - 4y ≤20 by shading.
4. Attempt any Nine Parts. 16
- The point (-5, 3) is the center of circle and point (7, -2) lies on it. Find radius of circle.
- Let P (x, y) = (-6, 9) and axis are translated through O'(-3,2) .Find translated coordinates of P.
- Find the equation of line bisecting first and third quadrant.
- Define centroid of triangle.
- Find the measure of angle between lines represented by x2 -xy- 6 y2 = 0.
- Find the equation of circle with center at (5, -2) and radius 4.
- Check the position of point (5, 6) w.r.t the circle x2 + y2 = 81 .
- Find the vertex and focus of parabola x2 = -16y .
- Find the foci and vertices of ellipse x2 +4y2 = 16.
- Find the vector from point A to origin when
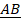 = 4
= 4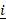 - 2
- 2 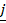 -
- 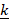 and B is the point (-2, 5).
and B is the point (-2, 5).
- Find the projection of
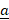 along
along 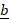 when
when 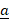 = 3
= 3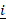 +
+ 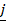 -
-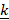 and
and 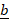 = -2
= -2 -
- 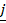 +
+ 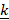
- Find
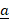 ×
× 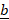 when
when 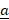 = [2,1,-1] and
= [2,1,-1] and 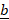 = [1,-1,1]
= [1,-1,1]
- Find the value of 2
 × 2
× 2 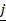 •
•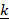
SECTION-II
Attempt any THREE questions. Each questions carries 10 'Marks.
Question#5
(a) Prove that 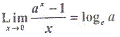
(b) Show that y = 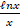 has maximum value at x = e.
has maximum value at x = e.
Question#6
(a) Evaluate ʃ 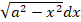
(b) Find the interior angles of the triangle whose vertices are
A(6,1)
B(2,7)
C(-6,-7)
Question#7
(a) Evaluate 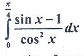
(b) Maximize the function f(x,y)= 20x+15y subject to constraints x+ y ≤ 100,
3x+ 2y ≥ 240, x≥ 0 ,y ≥ 0
Question#8
(a) Find equation of tangents to circle x2 +y2 = 2 and perpendicualr to line 3x+ 2y = 6
(b) Prove that in any triangle ABC, using vector method c2 = a2 + b2 -2tab cos C.
Question#9
(a) Write the equation of parabola whose focus (-3,1) , directrix x = 3.
(b) Find the area of the triangle determined by the points
P (0 ,0 ,0)
Q(2,3,2)
R(-1,1,4).