Untitled Document

Federal Board (2016)
MATHEMATICS HSSC-I
SECTION-A Marks 20)
Time allowed: 25 Minutes
NOTE: Section-A is compulsory and comprises pages 1-2. All parts of this section are to be answered on the question paper itself. It should be completed in the first 25 minutes and handed over to the Centre Superintendent. Deleting/overwriting is not allowe(D) Do not use lead pencil.

Q1. Circle the correct option i.e. A / B / C / (D) Each part carries one mark.

If ABC is an equilateral triangle then with the usual notations:

(A) r₁ r₂ r = r₃
(B) r₃ = 3r1r₂r₃
(C) 3r = r1 + r₂ + r₃
(D) 3r = r1 r₂ r₃

The value of cos|π-cos-1 ( )| is:

(A) -π
(B)
(C) π
(D) -

Which of the following is the simplified form of the complex number -7?

(A)
(B) -1
(C) 1
(D)

Let A and B two non-empty sets such that AB= Φ. Which of the following formula is true.

(A) n(A/B)=n(A)-n(B)
(B) n(AB)=0
(C) n(AB)= n(A)+n(B)
(D) n(AB)=n(A)-n(B)

Which of the following is the contra positive of the logical statement p→q?

(A) pq
(B) qp
(C) qp
(D) qp

Which of the following structure is true for the set of natural numbers under the multiplication?

(A) A monoid but a group
(B) A group
(C) A groupiod only
(D) A semi group but not monoid

What is the nature of roots of the quadratic equation x2- x -1=0?

(A) Rational and unequal
(B) Complex
(C) Real and equal
(D) Real and unequal

If A is a square matrix then which of the following argument is true.

(A) |A| = |-At|
(B) |A2| = |A|
(C) |A| =|-A|
(D) |A| = |At|

Which of the following is the solution (x,y) of the system of equations
?

(A) (2.0)
(B) Solution does not exist
(C) (0,1)
(D) (2.2)

Let one root of the equation ax2+ bx + c = 0 is 1 f . Then what will be the other root.

(A) -1+
(B) 2
(C) 1 -
(D) -1 -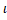

If an=(n+ 1)an where a1 = 1 then what will be a3?

(A) 8
(B) 10
(C) 4
(D) 12

The expression - is the resolved partial fraction of:

(A)
(B)
(C)
(D)

Let A.M and G.M between the two number a and b are equal. Then which of the following expression is equal to (a+ b)2.

(A) 2ab
(B)
(C) 4ab
(D) 4a2b2

If G.M between k and is is then what is the value of k?

(A) 4
(B) 2
(C)
(D)

If a die is rolled then what is the probability that the top is greater than 4?

(A)
(B)
(C)
(D)

What is the value of cosec2 100 cot2 1000:

(A) 0
(B) 2
(C) 1
(D) -1

The middle term of the expansion of (x -)12 is the :

(A) 8th term
(B) 5th term
(C) 6th term
(D) 7th term

The range of the function y=cot x is :

(A) R
(B) R/ lnπ’n є Z│
(C) -1 ≤ y ≤ 1
(D) y ≤ -1 or y ≤ 1

The value of cosec-1() is :

(A) 120°
(B) 150°
(C) -60°
(D) 30°

If one acute angle of a right angle triangle is 35o . Then the other acute angle is of measure:

(A) 45°
(B) 55°
(C) 145°
(D) 65°

MATHEMATICS HSSC-I
Time allowed: 2:35 Hours
Total Marks Section B & C: 80
NOTE: Section-'B' and 'C' comprises pages 1-2 and questions therein are to be answered on the separately provided answer book. Answer all questions from Section 'B' and Section ‘C’. Use supplementary answer sheet i.e. Sheet-B if require(D) Write your answers your neatly and legibly.

SECTION - B
(Marks 40)

2. Attempt any TEN parts. All parts carry equal marks. (10x4=40)

Express 1 + i in the polar form.
If S={ 1, -1, i, -i}. Set up its multiplication table and show that the set S is a group under multiplication
Solve the following matrix equations for A
A - = │
When x4 + 2x3 + kx2 + 3 is divided by x - 2 , the remainder is 1. Find the value of k.
If α, β are the roots of the equations 5X2 - x - 2 = 0 then from the equation whose roots are and
Resolve into partial fractions
How many terms of the series (-7) + (-4) + (-1) + ... .amount to 114?
Find values of n and r when nCr= 35 and nPr = 210.
Find the coefficient of xn in the expansion of (1 – x + x2 – x3 + ……..)2
Express the sexagasimal measure 75’ 6'30" into radian measurement.
Prove that
Show that sinx is a periodic function and its period is 2π.
Prove that with usual notations, R =
Show that 2tan-1 ()+tan-1 () =