(A) ![]()
(B)- ![]()
(C) –π
(D) π
Inter (Part-I) Gujrawala Board 2016
Mathematics
Part I (Objective Type)
Time Allowed: 30 Minutes
Max. Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(A)

(B)-
(C) –π
(D) π
(A)
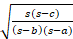
(B)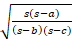
(C)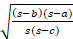
(D)
(A) 4π
(B) 2π
(C) π
(D) 3π
(A) 2
(B) 0
(C) 1
(D) -1
(A) n2
(B) 2n-2
(C) 2n-1
(D) 2n
(A) 0
(B) 3
(C) 2
(D) 4
(A) n+1Pr
(B) nPr+1
(C) n-1Pr
(D) nPr
(A)
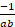
(B)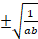
(C) ab
(D) -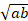
(A) 5
(B) -4
(C) 2
(D) 4
(A) { 0 }
(B) {0,ᶲ}
(C) {ᶲ,{0}}
(D) { {0},ᶲ}
(A) tan-1 A + tan-1 B
(B) cot-1 A + cot-1 B
(C) tan-1 A - tan-1 B
(D) cot-1 A - cot-1 B
(A) r=

(B) r=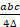
(C) r=
(D) r=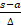
(A) 3 sin α - 4sin3 α
(B) 3 sin α + 4 sin3 α
(C) 4 sin3 α-3 sin α
(D) 4 sin3 α + 3 sin α
(A)
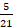
(B)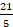
(C) 5
(D) 21
(A) null matrix
(B) identity matrix
(C) scalar matric
(D) diagonal matric
(A)
(B)
(C)
(D)
(A)
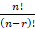
(B)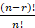
(C)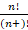
(D)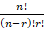
(A) proper fraction
(B) improper fraction
(C) identity
(D) decimal
(A) At
(B) A
(C) -At
(D) -A
(A) reflexive
(B) symmetric
(C) transitive
(D) commutative
Inter (Part-I) Gujrawala Board 2016
Mathematics
Part I (Subjective)
Time Allowed: 2.30 Hours
Max. Marks: 80
Section I
2. Write short answers to any EIGHT questions: (2x8=16)
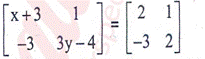
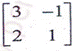
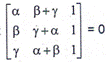
3. Write short answers to any EIGHT questions: (2x8=16)
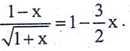
4. Write short answers to any NINE questions: (2x9=18)
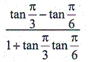
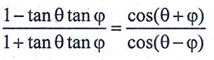
SECTION-II
NOTE: - Attempt any three questions. 10 x3=30
Question #5.
(a) Use Cramer's rule to solve the system (5)
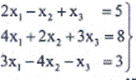
Question #6.
(a) Resolve into partial fractions: ![]() (5)
(5)
(b) Insert four harmonic means between the given numbers 4 and 20. (5)
Question #7.
(a) Find the numbers greater than 23000 that can be formed from the digits 1, 2, 3, 5, 6, without repeating any digit. (5)
(b) If ![]() …….., then prove that y2+2y-4=0 (5)
…….., then prove that y2+2y-4=0 (5)
Question #8.
(a) If cosec θ ![]() and m > 0(0<θ<
and m > 0(0<θ<![]() ), find the values of remaining trigonometric ratios. (5)
), find the values of remaining trigonometric ratios. (5)
(b) Prove that sin 10° sin 30° sin 50° sin 70° =![]()
Question #9.
(a) Prove that ∆ = r2 cot![]() cot
cot![]() cot
cot![]() (5)
(5)
(b) Prove that 2 tan-1 ![]() + tan-1
+ tan-1![]() =
=![]() (5)
(5)