(A) a-b=0
(B) a+b=0
(C) a+b>0
(D) a+b![]() 0
0
Inter (Part-II) Gujrawala Board 2016
Mathematics
Part II (Objective Type)
Time Allowed: 30 Minutes
Max. Marks: 20
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question.
Question #1
Circle the correct option i.e. A/B/C/D. Each part carries one mark.
(A) 4 k
(B) -4
(C) 0
(D) 4 i
(A) (a,o)
(B) (o,-a)
(C) (o,a)
(D) (-a,o)
(A) 2x-1>0
(B) 2x+1>0
(C) x+4<0
(D) 2x-1<0
(A) a-b=0
(B) a+b=0
(C) a+b>0
(D) a+b0
(A) cosec x + c
(B) – cosec x + c
(C) cot x + c
(D) – cot x + c
(A)
tan 2x
(B) tan 2x
(C)tanx
(D) 2 tan 2x
(A) x
(B)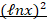
(C)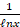
(D) ℓn(ℓnx)
(A) -3
(B) 1
(C) 0
(D) -1
(A) 1+
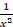
(B) 1-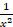
(C) 1+
(D) 1-
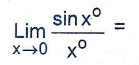
(A) 1
(B) 0
(C)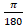
(D)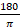
(A) a
(B) b
(C) c
(D)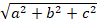
(A) A = 0, B
0
(B) AB
(C) A=B0
(D) C = 0
(A) 0
(B) 1
(C) 2
(D) 10
(A) ecosx
(B) esinx
(C) -sin x esin x
(D) - sin x ec°sx
(A) 3x3
(B) 3x2dv
(C) X3dv
(D) 3x2dx
(A)
π
(B) 0
(C) -1
(D) 1
(A)

(B)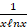
(C)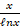
(D)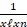
(A)
(B)
(C)
(D)
(A) 1
(B)
(C) 2
(D)
(A) sin x
(B) cos x
(C) cos hx
(D) sin hx
Inter (Part-I) Gujrawala Board 2016
Mathematics
Part I (Subjective)
Time Allowed: 2.30 Hours
Max. Marks: 80
Section I
2. Attempt any EIGHT parts. (2x8=16)
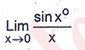
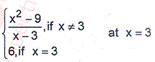
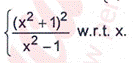
3. Attempt any EIGHT parts. (2x8=16)
4. Attempt any NINE parts. (2x9=18)
SECTION-II
NOTE: - Attempt any three questions. 10 x3=30
Question #5.
(a) Evaluate the ![]() (5)
(5)
(b)
Show that 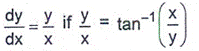 (5)
(5)
Question #6.
(a) Evaluate ![]() dx (5)
dx (5)
(b) Find an equation of the line through the intersection of the lines x - y - 4 = 0 and 7x + y +20 = 0 and parallel to the line 6x + y - 14 = 0 (5)
Question #7
(a) Evaluate ![]() (x3+3x2) dx (5)
(x3+3x2) dx (5)
(b) Graph the feasible region subject to the following constraint: (5)
2x-3y<6
2x+3<12
x> 0, y>0
Question #8.
(a) Prove vectorically that in any triangle ABC, a2 = b2 + c2 - 2bc cos A (5)
(b) Find equation of circle passing through A(4, 5), B( -4, -3), C(8, -3) (5)
Question #9.
(a) Show that the equation 9x2 _ 18x + 4y2 + 8y - 23 = 0 represents an ellipse. (5)
(b) Using vectors prove that the points A(-3, 5, -4), B(-1, 1, 1), C(-1, 2, 2) and D(-3, 4, -5) are coplaner. (5