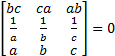Multan board Mathematic 2016
(Inter part-1)
(Mathematic)
(GROUP-1)
Note: Pour possible answers A, B, C and D to each question are given. The choice which you think is correct that circle in front that question with Marker or Pen ink. 'Lining or filling two or more circles 'will result in zero mat k in that question. Write the letter A, B. C or D in the column. (Write correct "option) against each question also. If there k a contradiction in the bubble and hand written answer, bubble option will be considered correct.
- Range of tan x is equal to:
- Q
- IR
- Z
- N
- If ABC be any triangle and
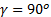 then,
then,
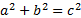
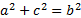
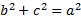
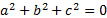
- Angle below the horizontal line is called:
- Right angle
- Oblique angle
- Angle of Elevation
- Angle of Depression
- Cos (
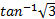 ) is equal to:
) is equal to:

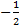

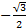
- {
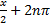 }
}
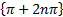
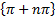
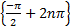
- The modulus of 1-i
 is equal to:
is equal to:
- - 2
- 2
- -
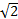
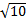
- Tabular form of a set
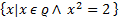 is equal to:
is equal to:
-
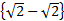
-
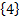
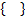
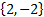
- If =
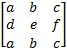 then det A is equal to:
then det A is equal to:
- 0
- 1
- (a - b)(c - a)
-
- The cofactor of an element
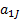 denoted by
denoted by 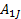 is equal to.
is equal to.

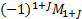
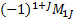

- A quadratic equation
 , becomes liner equation if:-
, becomes liner equation if:-
- a = 0
- b = 0
- c =0
- a=b
- Complex cube roots of -1 are:
-
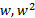
-
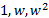
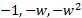

- Panel fractions of
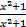 is equal to:
is equal to:
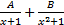
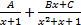
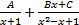
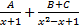
- If a, G, b be the G.P where a, b are numbers then G.M is equal to:
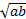
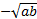
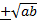
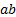
- A.P.
- G.P.
- H.P.
- None of these
- If S is a sample mace and E = S is on event then P (E) is equal to,
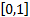
- 0
- 1
- (0.2)
- If
 =
= 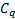 which of the following mat he true?
which of the following mat he true?
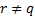
- r + q=n
- r – q + n
- q = 0
- 1+2x+3
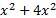 +------
+------ is the expansion of:-
is the expansion of:-
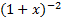

-
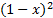
-
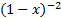
- Sum of exponent of a end b in
 in every term is:
in every term is:
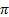
- 2
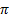


- The 60th part of 1- degree is called one:-
- Second
- Minute
- Degree
- Radian
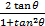 is equal to,
is equal to,
-
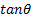
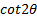
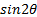
-
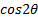
SUBJECTIVE PART
(Group 1)
(Section-I)
NOTE: Write same question number and its part number on answer book, as gives in the question paper.
Q2: Attempt any eight parts.
- Simplify
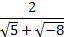 by expressing in the form a + bi
by expressing in the form a + bi
- Write
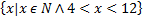 in descriptive and tabular form.
in descriptive and tabular form.
- Factorize a2+4b2
- Define Group.
- Write Reflexive Property of Equality of Real Numbers.
- Construct the truth table of of two statements p and q.
- Discuss the nature of the roots of equation x2+2x+3=0
- Find two consecutive numbers whose product is 132.
- Write any two properties of determinants of square matrices.
- Find the matrix X if X=
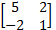 X=
X= 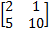
- Find the value of k if the polynomial
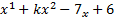 has a remainder of - 4 when divided by (x + 2).
has a remainder of - 4 when divided by (x + 2).
- If the matrices A and B are symmetric and AB = BA, show that AB is symmetric.
Q3. Attempt any eight parts.
- Resolve into partial fractions
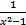
- Write the 1st three terms of the sequence if an =
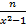
- Find A.M between
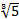 and
and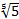 .
.
- Find the 12thterm of G.P if 1+ i, 2i, -2 +2i,-----
- Find the 9thterm of the H.P
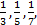 ------
------
- Write in factorial form

- Find the value of n when

- Show that
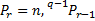
- Expand up to three terms
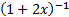
- Using Binomial theorem find the value up to three place of decimals of
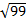
- Expand and simplify
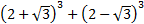
- Define Mutually Exclusive Events.
Q4. Attempt any nine parts.
- Find r when
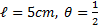 radian.
radian.
- Prove that
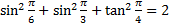
- Prove
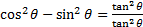
- If
 are the angles of a triangle ABC , then prove that Cos(
are the angles of a triangle ABC , then prove that Cos(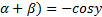
- Prove that Cos(
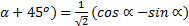
- Express Sin5
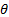 Cos2
Cos2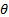 as sum or difference.
as sum or difference.
- Find the period of Cot8x
- Solve the right triangle, in which y=
 a =
a = 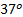 .
. 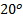 , a 243
, a 243
- With usual notations. prove that R =
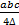
- Show that

- Without using calculator, show that
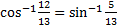
- Find the solutions of
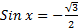 in
in 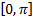
- Find the solutions of
 in
in 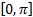
SECTION-II
NOTE: Attempt any three questions.
Q5:
- Solve the followings system of linear equation by Cramer’s rule: 2x + 2y + r=3, 3x – 2y -2z = 1, 5x +y -3z=?
- Show shot the roots of the following equation:- (x-a) (x-b) + (x-c)(x-a) are equal.
Q6:
- Resolve
 into partial fraction.
into partial fraction.
- Find four terms of A.P whose sum is 32 and sum of whose squares is 276.
Q7:
- In how many ways can be letters of the word MISSISSIPPI be arranged when all the letters are to be used?
- if x is very nearly equal to 1. then prove that p
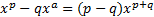
Q8:
- Prove that
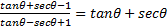
- Prove that sin10 sin30 sin50 sin70=
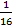
Q9:
- Prove that
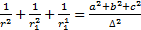
- Prove that

Multan board
Mathematic 2016
Inter part-1
(GROUP 2)
Note:Pour possible answers A, B, C and D to each question are given. The choice which you think is correct that circle in front that question with Marker or Pen ink. 'Lining or filling two or more circles 'will result in zero mat k in that question. Write the letter A, B. C or D in the column.(write correct "option) against each question also. If there k a contradiction in the bubble and hand written answer, bubble option will be considered correct.
- Range of
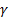 = Cos x is:-
= Cos x is:-
- R
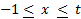
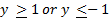
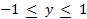
- With usual notations area of triangle ABC is:
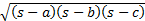 )
) 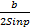
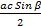
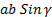
- With usual notation Iris
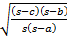
-
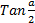
-
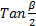
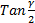
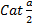


-


- Solutions of the equation 1 + Cos
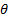 = 0 are in quadrants:-
= 0 are in quadrants:-
- I and IV
- II and III
- II and IV
- None of these
- Modulus of
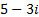 is:
is:
- 4
- 16
- 34
- 131
- Drawing conclusions from peruses believed to be true is called
- Induction
- Deduction
- Proposition
- Contradiction
- 1
- 2
- 3
- -3
- Every Diagonal matrix is also:-
- Triangular Matrix
- Scalar Matrix
- Rectangular Matrix
- Symmetric Matrix
- Recipmen1 Equation
- Transcendental Equation
- Quadratic Equation
- identity
- If the roots of
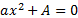 are real and unequal then:
are real and unequal then:
-
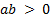
-
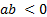

-
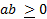
- Any improper rational fractional can be reduced to a mixed form by:
- Addition
- Multiplication
- Factorization
- Division
- With usual notations, the product of n Geometric Means between a and b is
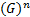
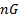
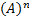
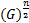
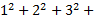 -------
-------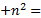
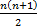
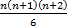
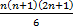

- If A and B are independent events then probability
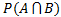 =
=
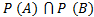
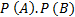
-
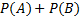
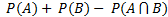
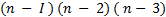 ------
------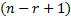 =
=
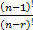
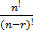
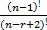
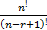
- There is no integer
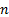 for which
for which 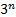 is:-
is:-
- Odd
- Even
- Prime
- Complex
- Expansion of
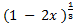 is valid if:
is valid if:

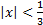
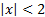

- An angle is said to be in standard position if its vertex is at:-
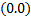

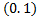

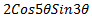 =
=
-
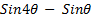
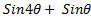
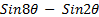
-

SUBJECTIVE PART
Mathematic
(Group 2)
(Section I)
Q2: Attempt any eight parts.
- Name the property used in
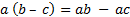
- Separate
 into real and imaginary pans.
into real and imaginary pans.
- Simplify
 .
.
- Write
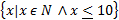 in the descriptive and tabular forms.
in the descriptive and tabular forms.
- Show that
 is a tautology.
is a tautology.
- Define a Group.
- Find the value of
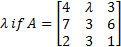 is singular.
is singular.
- Without expansion verify that
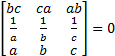
- If
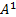 is symmetric. Show that
is symmetric. Show that is symmetric.
is symmetric.
- Prove that
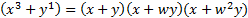
- If
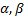 are the roots of
are the roots of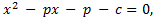 prove that
prove that
- Show that the roots of

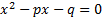 are rational.
are rational.
Q3: Attempt any eight parts.
- Resolve
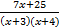 into Partial Fractions.
into Partial Fractions.
- Find the next two terms of 7. 9, 12. 16,
- If
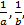 and
and  are in A.P. show that
are in A.P. show that 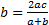
- Find the sum of infinite geometric series
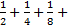 -----
-----
- If 5 is H.M. between
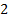 and
and 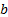 , find
, find 
- Evaluate
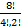
- How many 3 - digit number can be formed by using each one of the digits 2. 3, 5, 7, 9 only once?
- Find the value of /n, when

- A die is rolled. What is the probability that the dots on the top are greater than 4?
- Prove
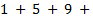 ----
----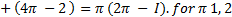
- Find the 60thterm in the expansion of
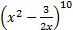
- If
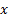 so small that its square and higher powers can be neglected. then show that
so small that its square and higher powers can be neglected. then show that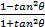
Q4. Attempt any nine parts.
- Verify
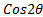 = I - 2
= I - 2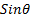 when
when 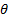 =
=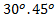
- Verify
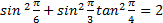
- Prove that
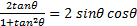
- If
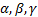 are the angles of a triangle ABC, then prove that
are the angles of a triangle ABC, then prove that 
- Prove that
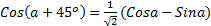
- Prove that Cos2
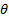 +=
+=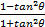
- Find the period of
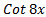
- Define in-circle.
- Prove that
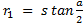
- Find
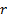 , if measures of the sides of triangle
, if measures of the sides of triangle 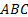 are
are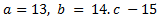
- Show that
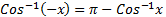
- Find the solution of
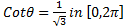
- Solve
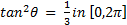
SECTION-II
NOTE: - Attempt any three questions.
Q5:
- Show that,
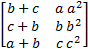 =
=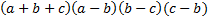
- Prove that
 =1 will have equal roots if =
=1 will have equal roots if =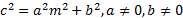
Q6:
- Resolve
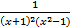 into partial fractions.
into partial fractions.
- For what value of
 is the positive geometric mean between
is the positive geometric mean between 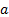 and
and 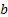 ?
?
Q7:
- Prove that
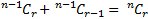
- If
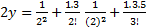 .
.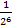 -------- then prove that
-------- then prove that 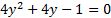
Q8:
- Prove the identity
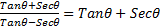
- Prove that
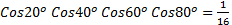
Q9:
- The sides of a triangle
 and
and 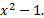 Prove that the greatest angle of the triangle is
Prove that the greatest angle of the triangle is 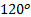
- Prove that