Multan Board 2016
INTERMEDIATE PART-II (12th CLASS)
MATHEMATICS
TIME ALLOWED: 30 Minutes
MAXIMUM MARKS: 20
OBJECTIVE
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
(A)
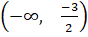
(B)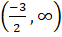
(C)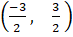
(D)
(A) x2 - y2 = r2
(B) x2 + y2 = r2
(C) y2 - x2 = r2
(D)+
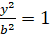
(A)
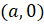
(B)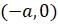
(C)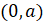
(D)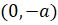
(A)
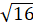
(B)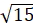
(C)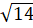
(D)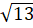
(A)
,
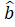
(B)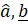
(C)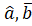
(D),
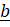
(A) 1
(B) 4
(C) 6
(D) 8
(A)

(B)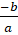
(C)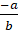
(D)
(A)
2
(B)2
(C)2
2
(D)2
2
(A)
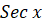
(B)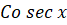
(C)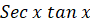
(D)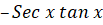
(A) 2x
(B)x
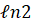
(C) 1/2x
(D)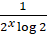
(A)
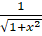
(B)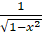
(C)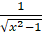
(D)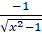
(A)
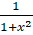
(B)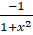
(C)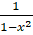
(D)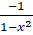
(A)
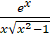
(B)x
-1
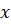
(C)xCosee-1
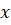
(D)x
-1
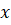
(A)
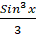
(B)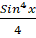
(C)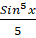
(D)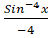
(A)
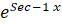
(B)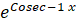
(A)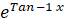
(A)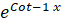
(A) 0
(B) 4
(C) 8
(D) 16
(A)
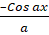
(B)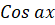
(C)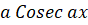
(D)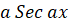
(A)
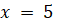
(B)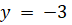
(C)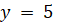
(D)
(A) Slope intercept form
(B) Two intercept form
(C) Symmetric form
(D) Normal form
(A)
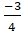
(B)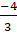
(C)
(D)
Time: 2:30 Hours (Subjective Part)
Marks: 80
SECTION-I
GROUP-I
NOTE: - Write same question number and its part number on answer book as given in the question paper.
2. Attempt any eight parts.

3. Attempt any eight parts.
4. Attempt any nine parts.
SECTION-II
NOTE: - Attempt any three questions.
5.(a) 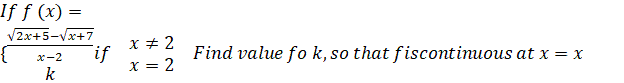
(b) ![]() (
(![]() (
(![]() prove that
prove that ![]() 2
2 ![]() +
+![]()
6.(a) Evaluate ![]()
(b) The vertices of a triangle are ![]() and
and ![]() Find coordinates of orthocentre.
Find coordinates of orthocentre.
7. (a) Solve the differential equation (![]() 2 —
2 — ![]() 2 )
2 ) ![]() 2 —
2 — ![]() 2= 0
2= 0
(b) Maximize ![]() subject to the constraints
subject to the constraints ![]()
![]() ,
, ![]()
![]() ,
,![]() 0, y
0, y![]() 0
0
8. (a) Write an equation of circle which passes through the points ![]()
(b) Find the vector from the point ![]() to the origin when
to the origin when ![]() and
and ![]() is the point
is the point ![]()
9.(a) Find equation of parabola with given elements, focus ![]() and directrix
and directrix ![]()
![]()
(b) In any triangle![]() , prove that by vector method
, prove that by vector method![]() =
=![]() =
=![]()
Multan Board 2016
INTERMEDIATE PART-II (12th CLASS)
MATHEMATICS PAPER-II
TIME ALLOWED: 30 Minutes
MAXIMUM MARKS: 20
OBJECTIVE
Note: You have four choices for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
(A)
2
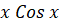
(B)2
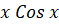
(C)
(D)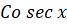
(A)
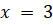
(B)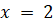
(C)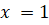
(D)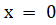
(A)
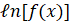
(B)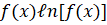
(C) -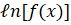
(D)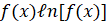
(A)
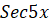
(B)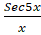
(C)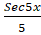
(D)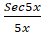
(A)
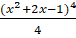
(B)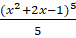
(C)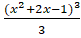
(D)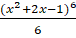
(A)

(B)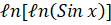
(C)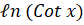
(D)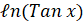
(A)
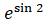
(B)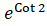
(C)
(D)
(A)
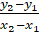
(B)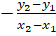
(C)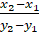
(D) -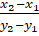
(A)
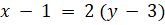
(B)
(C)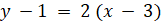
(D)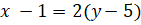
(A)
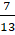
(B)
(C)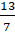
(D)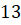
(A)
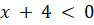
(B)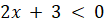
(C)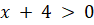
(D)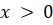
(A)
2
2
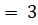
(B)2 +
2
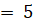
(C)2
2
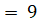
(D)2
2
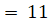
(A)
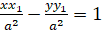
(B)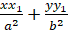
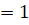
(C)1 –
1 =0
(D)1+
1 =0
(A)
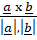
(B)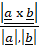
(C)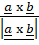
(D)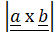
(A)
=0
(B)=0
(C)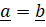
(D)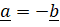
(A) (
)
(B) [-1,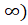
(C) [0,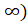
(D) [-1,1]
(A)

(B) 2
(C) 3
(D)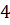
(A)
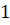
(B)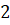
(C)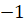
(D)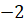
(A)
2
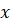
(B)2
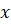
(C)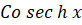
(D)2
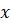
(A)
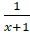
(B)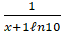
(C)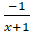
(D)
Time: 2:30 Hours (Subjective Part)
Marks: 80
SECTION-I
GROUP-II
NOTE: - Write same question number and its part number on answer book as given in the question paper.
2. Attempt any eight parts.
3. Attempt any eight parts.
4. Attempt any nine parts.
SECTION-II
NOTE: - Attempt any three questions.
5.(a) ![]()
(b)![]() ,
, ![]() then prove that
then prove that ![]()
6.(a) Evaluate ![]()
(b) Show that distance of the point ![]() (x1, y1) from the line
(x1, y1) from the line ![]() is
is ![]()
7. (a) Evaluate ![]()
(b) Minimize ![]() subject to constraints
subject to constraints ![]()
![]() 15
15![]()
![]()
![]()
![]()
8. (a) Show that the circles ![]() 2
2 ![]() 2
2 ![]() and
and ![]() 2
2 ![]() 2
2 ![]() touch externally.
touch externally.
(b) Prove that the line segments joining the mid points of the sides of a quadrilateral taken in order form a parallelogram using Vector Method.
9.(a) Find the focus, vertex and directrix of the parabola ![]() 2
2![]()
(b) Find the moment about ![]() of each of the concurrent forces
of each of the concurrent forces ![]() - 2
- 2![]() , 3
, 3![]() +2
+2![]() -
-![]() ,5
,5![]() +2
+2![]() where
where ![]() is their point of concurrency.
is their point of concurrency.