Rawalpindi board (2016)
Mathematics (objective Type)
Time: 30 Minutes
Marks: 20
Note: Four Answers are given against each column A,B,C &D. Select the write answer and only separet answer sheet, fill the circle A,B,C or D with pen or marker in front of that question number.
- If Z is a complex number, then |Z|2 is:
(a) Z2
(b) (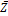 )2
)2
(c) Z
(d) 
- For any two sets A and B, (A∩ B)’ is equal to:
(a) A'
(b) B'
(c) A'U B’
(d) A ∩ B
- The multiplicative identity in the set of real numbers is:
(a) Zero
(b) 1
(c) 3
(d) 2
- A square matrix A =[aij] with complex entries is called skew Hermitian if (
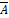 )t is equal to:
)t is equal to:
(a) A
(b) -A
(c)|A|
(d) -|A|
- If A and B are any two non singular matrices such that (AB)-1 is equal to:
(a) A‑1 B-1
(b) B-1 A‑1
(c) BA
(d) AB
- A reciprocal equation remains unchanged when variable x is replaced by:
(a) 
(b) 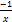
(c) 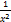
(d) –x
- The roots of equation
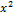 - 5x + 6 = 0 are:
- 5x + 6 = 0 are:
(a)2. -3
(b) -2 , 3
(c) 2, 3
(d) -2 , 3
- (x -1)2 = x2 – 2x +1 is called:
(a) Equation
(b) Conditional
(c) Identity
(d) Fraction
- A.M between
 and 5
and 5 :
:
(a) 4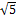
(b) 5
(c) 10
(d) 2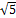
(a) a1yn
(b) a1yn-1
(c)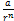
(d) 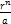
- If n = 1, then value of n|n –1 is
(a) Zero
(b) 1
(c) 2
(d) -1
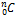 equals :
equals :
(a) 1
(b) n
(c) Zero
(d) 2
- General term of expansion (a + x)" is:
(a)  an-r xr
an-r xr
(b) 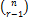 an-r xr
an-r xr
(c) 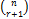 ar xn-r
ar xn-r
(d) 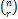 an-r xr
an-r xr
- The sum of binomial co -efficients in the expansion of (1 + x)4 is:
(a) 8
(b) 10
(c) 16
(d) 32
- cos22
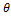 + sin2 2
+ sin2 2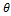 is equal to:
is equal to:
(a) 1
(b) Zero
(c) sec2 0
(d) 2
- cos (π/2- β) is equal to:
(a) sin β
(b) - sin β
(c) cos β
(d) - cos β
(a) 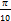
(b) 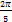
(c) 
(d) 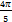
- For any triangle ABC, with usual notations r2 is equal to:
(a)
(b) 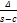
(c) 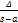
(d) 
- tan (sin-1 x) is equal to:
(a) 1+ 2x2
(b) 1–x2
(c)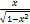
(d)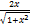
- The solution of equation –2+ sin
 = 0 are in quadrant.
= 0 are in quadrant.
(a) I &IV
(b) I & III
(c) III & IV
(d) II & IV
Rawalpindi board (2016)
part I
Mathematics (Subjective type)
Time: 2:30 Hours
Section-I
Marks: 80
2. Attempt any Eight Parts.16
- Find the multiplicative inverse of (-4 7)
- Find real and imaginary parts of (
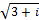 )3.
)3.
- Define equivalent sets.
- Define monoid.
- Find the inverse of the matrix A =
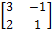 .
.
- Show that
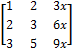 = 0 without expansion.
= 0 without expansion.
- Find the value of λif A =
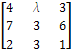 is singular.
is singular.
- Define exponential equation.
- If U = {1,2,3,…….10} , A = {2,4,6……..20} and B = {1,3,5……. 19} , prove that (AUB)’= A’ ∩B’
- Write converse and contrapositive of the conditional Nq
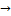 Np.
Np.
- Find there cube-cube roots of unity.
- If a, β are the roots of 3x2-2x+4= 0, find the values of
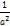 +
+  .
.
3.Attempt any Eight Parts. 16
- Resolve
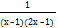 into partial fractions.
into partial fractions.
- Which term of the A.P 5,2,-1....is -85.
- Find the value of n if nP4 : P = 9 :1.
- Find the number of diagonals of 12 sided figure.
- Find the first four terms of (1 + 2x)-1.
- Find the 6th term in the expansion of
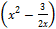 10
10
- Find the next two terms of the sequence 1,-3,5,-7,9,-11,…….
- If 5,8 are two A.Ms between a and h find a and b.
- Convert the recurring decimal 2.
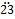 into the equivalent common fraction.
into the equivalent common fraction.
- Convert n(n –1)(n – 2)…..(n – r + I) in the factorial form.
- How many numbers greater than 1000,000 can be formed from digits 0, 2, 2, 2, 3, 4, 4.
- Show that inequality 4n > 3n + 4 is true for n = 2,3.
4. Attempt any Nine Parts.18
- Verify 2 sin 45° +
 cosec 45° =
cosec 45° =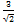
- Prove that: cot2
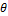 - cos2
- cos2 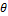 = cot2
= cot2 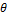 cos2
cos2 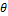
- Find the value of tan 75° (without calculator).
- Prove that: cos 306° + cos 234° + cos 162° + cos 18° = 0.
- Prove that
 =
= 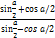
- Prove that: sin
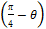 sin
sin  =
=  cos2
cos2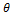 .
.
- Find the period of cos ec x/4 .
- Show that: tan (sin-1 x) =
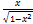 .
.
- Prove that abc (sin a + sin β + sin
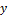 ) = 4S .
) = 4S .
- Define trigonometric equation.
- Find the area of triangle ABC, if a = 524, b = 276, c = 315.
- Find the smallest angle of the triangle ABC, when a = 37.34,b= 3.24, c = 35.06.
- Find the solution of secx=-2 which lies in [0,2
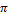 ].
].
SECTION-11
Attempt any THREE questions. Each questions carries 10 marks.
5.(a) Use Cramer's rule to solve the system:
2x + 2y + z = 3 ; 33x – 2y -2z = 1 ; 5x +y – 3z = 2
(b) If a and β are the roots of x2-3x+5 = 0 from the
equation whose roots are 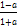 and
and 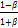 .
.
6.(a) Resolve into partial fractions.
(b) For what value of n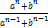 is G.M between a and b.
is G.M between a and b.
7.(a) How many arrangements of the letters of the word ATTACKED can be made if each arrangement begins with and ends with K.
(b) Find the co-efficient of x5 in the expansion of 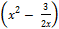 10
10
8.(a) Prove the identity
sin6 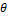 – cos6
– cos6 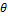 = (sine2
= (sine2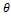 –cos2
–cos2 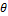 )(1–sine2
)(1–sine2  cos2
cos2 ).
).
(b) If sin a= and cos
and cos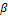 =
=  where 0 < a < π/2 and
where 0 < a < π/2 and
0<β< show that sin (a-β) =
show that sin (a-β) = 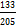
9.(a) The sides of a triangle are x2+ x +1,2x +1 and x2 -1 prove
that the greater angle of the triangle is 120°.
(b) Prove that tan-1  + tan-1
+ tan-1  = tan-1
= tan-1  + tan-1
+ tan-1  .
.
![]() )2
)2![]()
![]()
)2


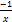
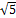
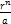
an-r xr
an-r xr
ar xn-r
an-r xr
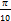
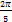

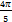

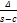

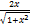
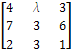 is singular.
is singular.![]() and
and ![]() .
.![]()
![]() is G.M between a and b.
is G.M between a and b.![]() 10
10![]() – cos6
– cos6 ![]() = (sine2
= (sine2![]() –cos2
–cos2 ![]() )(1–sine2
)(1–sine2 ![]() cos2
cos2![]() ).
).![]() and cos
and cos![]() =
= ![]() where 0 < a < π/2 and
where 0 < a < π/2 and![]() show that sin (a-β) =
show that sin (a-β) = ![]()
![]() + tan-1
+ tan-1 ![]() = tan-1
= tan-1 ![]() + tan-1
+ tan-1 ![]() .
.