RAWALPINDI BOARD 2016
PAPER MATHEMATICS
PART -2
Time:30 Min.
(Objective Part)
Marks: 20
Note: Four Answers are given against each column A,B,C & D. Select the write answer and only separate answer sheet, fill the circle A,B,C, or D with pen or maker in front of that question number.
(a)
(b) –
(c) cosec 2x
(d) – cosec x cot x
(a) ex
(b) 1
(c) x
(d) 1/x
(a) π
(b) π/6
(c) π/4
(d) π/2
(a) 5
(b) 4
(c) 2
(d) 0
(a) 1
(b) x2
(c) x4
(d)
(a) x = -3
(b) x= -
(c) x = 0
(d) x = 1
(a) 2cosx2
(b) cos x2
(c) 2x cos2 x
(d) 2 cos x2
(a) -
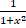
(b)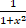
(c)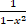
(d)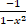
(a) cos2 x
(b) sin2 x
(c) cosec2 x
(d) cot2 x
(a) Centre
(b) Vertex
(c) Directix
(d) Major-axis
(a) (-a , a)
(b) (a , -a)
(c) (a , a)
(d) (-a , -a)
(a) 1
(b) -1
(c) 0
(d) 2
(a) 90°, 90°, 45°
(b) 0°, 0°, 45°
(c) 45°, 45°, 90°
(d) 30°, 30°, 30°
(a) sin 2x
(b) 2sin 2x
(c)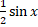
(d) 2 sin x
(a) ℓogx
(b) ℓog(ℓogx)
(c)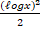
(d)
(a) ℓn sin π/4
(b) 1
(c) sec2 π/4
(d) x tan π/4
(a) sin p sec2x
(b) sin p tan x
(c) cos p sec2x
(d) sec2 x
(a) 2:1
(b) 1:2
(c) 1:1
(d) 3:2
(a) 45°
(b) 30°
(c) 60°
(d) 75°
(a) 0 < x < 4
(b) 10 < x < 15
(c) -∞ < x < 4
(d) 4 < x < ∞
Time:30 Min.
(Subjective Part)
Marks: 80
Note: Four Answers are given against each column A,B,C & D. Select the write answer and only separate answer sheet, fill the circle A,B,C, or D with pen or maker in front of that question number.
Section-1
2. Attempt any Eight Parts.
2. Attempt any Eight Parts.
4. Attempt any nine Parts.
Section-2
Attempt any three questions, each question carries 10 marks.
5. (a) Evaluate ![]()
![]() .
.
(b) If y = a cos (![]()
![]()
6. (a) Evaluate: ![]()
(b) Find h such that the points A(![]() ,-1), B(0,2), C(h,-2) are the vertices of a right triangle with right angle at the vertex A.
,-1), B(0,2), C(h,-2) are the vertices of a right triangle with right angle at the vertex A.
7. (a) Find the area between the X-axis and the curve y=![]() when >0
when >0
(b) Find the maximum value of ƒ(x) = 4x+6y under the constraints.2x-3y ≤ 6, 2x + y ≤2, 2x+3y ≤12, x ≥y ≥0.
8. (a) Find the equation of the tangents to the circle x2+y2=2 parallel to the line x-2y+1=0.
(b) Find the number Z, so that the triangle with vertices A(1,-1,0), B(-2,2,1) and C(0,2,Z) is a right angle triangle with right angle at C.
9. (a) Find an equation of the parabola whose focus is F(-3,4) and directrix is 3x-4y+5=0.
(b) Find the value of α so that ![]() and 2
and 2![]() are complainer.
are complainer.