SAHIWAL BOARD 2016
PAPER MATHEMATICS PART-II
Time: 30 Minutes
(Objective Part)
Marks:20
Note: Four Answers are given against each column A,B,C & D. Select the write answer and only separate answer sheet, fill the circle A, B ,C or D with pen or marker in front of that question number.
(A)
In a
(B)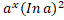
(C)x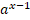
(D).Ina
(A) sinh x
(B) -sinhx
(C) cosech x
(D) coth x
(A) d
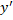
(B)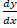
(C)dy
(D) dx
(A) Sin x
(B) cos x
(C) –cos
(D) -sinx
(A)
(B)
(C)
(D)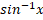
(A)
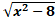
(B)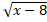
(C)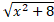
(D)
(A)
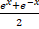
(B)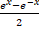
(C)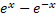
(D)
(A)
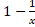
(B)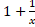
(C)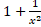
(D)
(A)
(x)
(B) 5
(C) 5(x)
(D) f(x)
(A) 2x-3>0
(B) 2x+3<0
(C) x+4<0
(D) x<0
(A) (-1,-3)
(B) (-1,3)
(C) (1,-3)
(D) (1,3)
(A) (a,0)
(B) (-a,0 )
(C) (0,a)
(D) (0,-a)
(A)
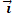
(B)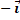
(C) 1
(D) 0
(A)
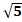
(B) 5
(C) 25
(D) 30
(A)
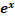
(B)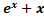
(C)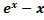
(D)
(A) 6x+2
(B)x3+x2
(C) 3x+2
(D)+
(A) 7
(B) 3
(C) -3
(D) -7
(A) 0
(B)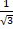
(C)1
(D)
(A) Circle
(B) Ellipse
(C) Parabola
(D) Straight Line
(Subjective Part)
Marks: 80
SECTION-I
2. Attempt any Eight Parts.
3. Attempt any Eight Parts.
SECTION-II
Note:Attempt any THREE questions. Each questions carries 10 marks.
Q.No.5.
(a) If f(x)= ![]() Find the value of k so that f is continuous at x = 2.
Find the value of k so that f is continuous at x = 2.
(b) Show that ![]() =
=![]() if
if![]()
Q.No.6.
(a) Evaluate ![]() dx
dx
(b) Find the equation of perpendicular bisector of the segment joining the points A (3,5) and B (9,8)
Q.No.7.
(a) Evaluate: ![]()
(b) Graph the feasible region constrained by 2x-3y≤6,2x+y≥2, x+2y≤8,x≥,y≥ 0
Q.No. 8.
(a) Find an equation of the circle which passes through the points A(5,10) , B (6,9) , C (-2,3).
(b) Using vectors method prove that cos(α + β) = cosα cosβ -sinα sinβ
Q.No.9.
(a) Find focus, vertex, and directrix of parabola x2 -4x-8y+4=0.
(b) Find the moment about A(1,1,1) of each of the concurrent forces ![]() -2
-2![]() -,3
-,3![]() +2
+2![]() -k,5
-k,5![]() +2
+2![]() where P (2,0,1) is their point of concurrency.
where P (2,0,1) is their point of concurrency.