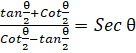Bahawalpur Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- (-ι)19is equal to:
(A) -i
(B) i
(C) 1
(D) -1
- If A= { } then P (A) is equal to:
(A) { }
(B) { 0 }
(C){{ }}
(D) {0, 1 }
- if
 = 0, then
= 0, then =…………
=…………
(A) 3
(B) -3
(C) 
(D)3
- (A-1)t is equal to:
(A)A
(B)A-1At
(C) -At
(D)(At)-1
- Complex Cube Roots of -1 are:
(A)W,W2
(B) 1,w,w2
(C)-1,-w,-w2
(D) 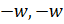
- For a Quadratic Equation ax2 + bx + c = 0, then product of roots is:
(A) 
(B) - 
(C) 
(D)ac
- The Fraction
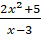 is:
is:
(A) Proper
(B)Rational
(C)Polynomial
(D)Improper
- Arithmetic Mean between 3
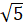 and 5
and 5 is:
is:
(A)4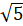
(B)5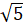
(C) 10
(D) 2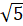
- is equal to:
(A)1
(B) n
(C) n2
(D) n3
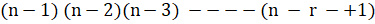 =------------:
=------------:
(A) 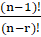
(B) 
(C) 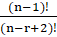
(D) 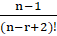
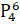 is equal to:
is equal to:
(A)160
(B)260
(C)360
(D)340
- Sum of Binomial Coefficients is:
(A) n
(B)2n
(C) 2n
(D)n2
- In Expansion (a + b) 7, the 2nd Term is:
(A) a7
(B) 7a6b
(C)7ab
(D) 0
- One Radian is equal to:
(A)56.296°
(B) 57°
(C) 56°
(D) 0.175°
- Sin (
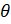 + 270°) = -------:
+ 270°) = -------:
(A)Cot 
(B) Tan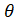
(C) Sin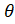
(D)-Cos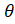
- Period of Sin
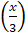 is----------:
is----------:
(A) 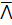
(B) 3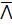
(C)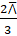
(D)6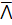
- If
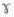 = 90°, then with usual notation ---:
= 90°, then with usual notation ---:
(A)c2=a2+b2
(B) b2=a2+c2
(C) a2=b2+c2
(D)a2-b2=c2
- R is equal to:
(A) 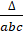
(B) 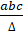
(C) 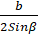
(D) 
- Cos(tan-1
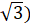 =
=
(A)
(B) 
(C) 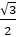
(D) 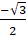
- Cosx =
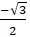 then Reference Angle of Cos x is:
then Reference Angle of Cos x is:
s
(A) 
(B) 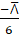
(C) 
(D) 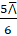
Bahawalpur Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 2.10 Hours
MAXIMUM MARKS: 60
SUBJECTIVE
1. Attempt any Eight of the following. All carry equal marks.
SECTION-I
- State Trichotomy Property and Transitive Property of Insequality.
- Define Monoid Group.
- What is the difference between {a, b} and { {a, b} }?
- Construct the Truth Table of [(p
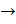 q^p
q^p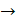 q)].
q)].
- If w is a Cube Root of Unity, form an equation whose roots are
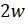 and
and 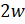 2.
2.
- A number exceeds its square root by 56. Find the Number.
- Show that the roots of x2+ (mx+ c)2 will be equl, if c2 = a2(1+m2)
- if z1 = 2 + i, z2 3 - 2i, z3 = 1 + 3i then express
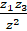 in the form of a + ib.
in the form of a + ib.
- Separate =
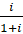 into Real and Imaginary Parts.
into Real and Imaginary Parts.
- Show that (AB)t = Bt At if
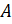 =
= 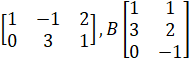
- If A=
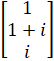 and (
and (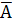 )t
)t
- Without Expansion show that
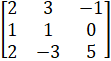 = 0
= 0
3. Attempt any eight parts.
- Define Improper Rational Fracition.
- Insert two G.Ms between 2 and 16.
- Show that G2= AH if a 9, b = 4.
- Find number of Diagonals in 8 sided figure.
- Prove that n4 > 3n + 2n-1, for n = 2, 3
- Find n, when
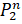 = 30
= 30
- Which term of the A,P,5,2,-1, --- is - 85?
- Simplify (2 + i)5
- Write the first four terms of the Sequence, if an =
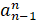 ,a1 = 1
,a1 = 1
- There are 5 Green and 3 Red Balls in LI Box. One ball is taken out. What is the probability that the ball is Green?
- How many Necklace can be made from 6 heads of different colors?
- Neglecting x2 and higher powers of "x", show that
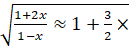
4. Attempt any six parts.
- Find
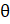 ,when 1= 3.2m, r = 2m
,when 1= 3.2m, r = 2m
- Prove that Tan (180° +
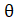 ) = Tan
) = Tan 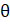
- Express 2 Cos 5
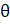 Sin5
Sin5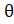 as Sums or Difference.
as Sums or Difference.
- Find the Period of Cot
 .
.
- Find the Area of Triangle ABC if a= 18, b= 24, c = 30
- It measure of Sides of Triangle ABC are a = 13, b = 14, c = 15 find R.
- Show that Sin(2 Cos-1x) =
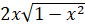
- Solve 2Sin2
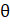 = 0 for 5
= 0 for 5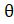
- If Cot
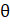 =
=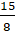 and Terminal Arm of Angle is not in Quad-1, find the values a f Cos
and Terminal Arm of Angle is not in Quad-1, find the values a f Cos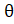 and Cosec
and Cosec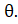
- Prove the Identity (Sec
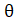 - Tan
- Tan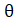 ) = 1
) = 1
- Shaw that Cos(
 -
-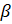 )= Sin
)= Sin 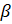
- A ladder leaning against a vertical wall makes an angle 24° with the wall. Its foot is 5m from the wall. Find its length.
- Find the solution of Sin x = -
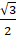 which lie in [0, 2
which lie in [0, 2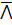 ]
]
SECTION-II
NOTE: - Attempt any three questions.
5. (a) Let G be the set of all 2 x 2 Non-Singular Real Matrices. Then under the usual Multiplication of Matrices G is a non-abelian group.
(b) Show that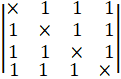 =(x+ 3) (x- 1)3
=(x+ 3) (x- 1)3
6. (a) Solve the System of Equation 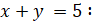 + x2+2y2 = 17
+ x2+2y2 = 17
(b) Resolve 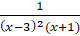 into Partial Fractions.
into Partial Fractions.
7. (a) If a2. b2 and c2 are in A.P., show that  ,
,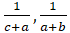 are in A.P.
are in A.P.
(b) Find the term Independent of x of 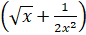 10
10
8. (a) Prove that 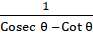 -
-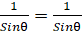 -
-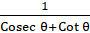
(b) Prove the given Identity: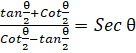
9. (a) Prove that 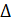 = 4R r Cos
= 4R r Cos Cos
Cos 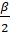 Cos
Cos
(b) Prove that Sin-11/√5+cot-1x=π/2
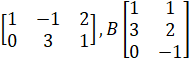
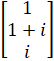 and (
and (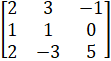 = 0
= 0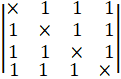 =(x+ 3) (x- 1)3
=(x+ 3) (x- 1)3