DHERA GHAZI KHAN Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes Group-1
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
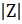 2=-
2=-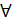 Z
Z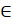 C
C
(A) Z2
(B) 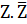
(C)(C)( )2
)2
(D) Z
- The contra positive of P
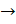 q is:
q is:
(A) -P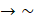 q
q
(B) 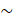 q
q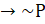
(C) q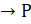
(D) 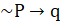
- If A is a square matrix of order 3, then IKAI =
(A)K IAI
(B)K2 IAI
(C)K3 IAI
(D)K4 IAI
- If ord (A) = m x n , ord (B)= n 4 then ord (AB)T is
(A) m n
n
(B) m m
m
(C)p m
m
(D)p x n
- Roots of Px2 - qx + r = 0 are equal if:
(A) P = qr
(B) Pq = r
(C)q2 = 4pr
(D)r2= P
- x3 – 3x2 + 2x
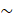 6 has factor:
6 has factor:
(A)x-4
(B)x - 3
(C)x + 3
(D)x+2
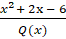 is improper if:
is improper if:
(A)Degree of Q(X)=2
(B) Degree of Q(X)=3
(C)Degree of Q(X)=4
(D)Degree of Q(X)=5
- The series a+ar +ar2+…….
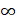 is convergent if:
is convergent if:
(A)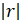 >1
>1
(B)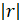 <1
<1
(C) 
(D) 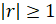
- Common ratio of geometric sequence cannot be:
(A) 0
(B)1
(C)3
(D)2
- If a die rolled, then n(S)=
(A) 6
(B) 36
(C)9
(A 2
- n! >2n -1 is valid if:
(A)n=3
(B) n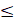 3
3
(C) n<4
(D) n
- Expansion of(1-2x)1/3a is valid if:
(A) 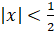
(B) 
(C) 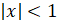
(D) 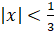
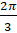 radians equals to:
radians equals to:
(A) 150°
(B)130°
(C)270°
(D) 120°
- Sin(-300°) =
(A) 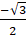
(B) 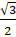
(C) 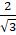
(D) 0
- Period of Tan
 is:
is:
(A) 
(B) 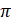
(C) 2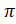
(D) 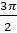
- If in a
 ABC, a = b = c, then
ABC, a = b = c, then
(A) 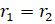
(B) 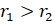
(C) 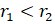
(D) 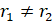
- Sec
 =:
=:
(A) 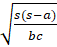
(B) 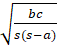
(C) 
(D)
- Tan (Tan-1(-1) =
(A) 1
(B) 
(C) -
(D) -1
- If sec x = -2, reference angle is:
(A) 
(B) 
(C) -
(D) 
DHERA GHAZI KHAN Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
(Subjective Type)
Time Allowed: 2:30 Hours Group-1
Maximum Marks: 80
NOTE:- Write same question number and its part number on answer book. As given in the question paper.
SECTION-I
2. Attempt any eight parts.
- Simplify by justifying each step
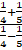
- Separate into real and imaginary parts
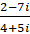
- Prove that
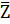 = Z if f Z is real.
= Z if f Z is real.
- Verify the commutative property of union and intersection for sets A = 1,2,3,4,5), B = {4,6,8,10)
- Define conditional
- Find the inverse of the relation{(x,y)/y2= 4ax,x > 0)
- Solve the system of linear equation
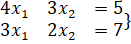
- If A=
 and B =
and B = 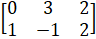 Find 4A 3B.
Find 4A 3B.
- Find the value of
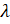 if A is singular Matrix where A =
if A is singular Matrix where A =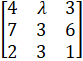
- Solve x(x+7) = (2x-1) (x+4) by factorization
- Show that x3 – y3 = (x-y) (x-Wy(x-W2y)
- Find the condition that one root of x2 + Px + q = 0 is multiplication inverse of the other
3. Attempt any eight parts.
- Convert into proper form
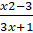
- Find next two terms of 7, 9, 12, 16,………..
- Find three A.Ms between
 and 3
and 3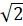
- Insert two G.Ms between 2 and 16
- Find sum of first 15 terms of G.P. 1,
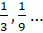 ……….
……….
- Evaluate
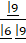
- How many arrangements of the word "MATHEMATICS" taken all together
- Evaluate of
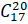
- If S = {I,2,3,……. 9}, A = (2, 4, 6, 8), B= (I, 3, 5), find P(AUB)
- 1+5+9+ ..... +(4n-3)= n(2n-1) Prove for n = I,2
- Find 5th term of (3x/2-1/3x)11
- Expand unto 3 terms of (8 – 5x)-2/3
4. Attempt any six parts.
- Find
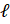 , when
, when 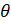 =
= 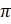 radians, r = 6 cm
radians, r = 6 cm
- In which quadrant are the terminal arms of the angle lie when sin
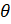 <0 and Cos
<0 and Cos 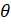 >0
>0
- Verify the following 2 Sin45°+
 Cosec 45°=
Cosec 45°=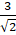
- Prove that Cos (
 2 -
2 -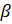 ) = sin
) = sin 
- Prove that Sin 75° =
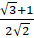
- Find the value of Cos 105°
- Find the period of Cosec (10x)
- State "The Law of Cosines"
- Show that R =
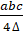
- Show that r2= s tan
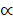 /2
/2
- Without using table/Calculator, show that tan-1 5/12 = sin-15/13
- Find the solutions of Cosec
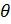 = 2in [0, 2
= 2in [0, 2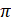 ]
]
- Solve the trigonometric equation Cosec2
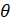 = 4/3
= 4/3
SECTION-II
NOTE: - Attempt any three questions.
5. (a) Show that the set S = { 1, -1, i, -i) is an abelian group under Multiplication where i2 = -I
(b) Show that 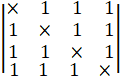 = (x + 3)(x -1)3
= (x + 3)(x -1)3
3x + 4y = 25
6. (a) Solve the equation 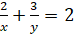
(b) Resolve 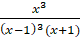 into partial fractions
into partial fractions
7. (a) Sum the series : 2 + (1 - 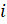 )+
)+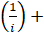 …. to 8 terms
…. to 8 terms
(b) Determine the middle term in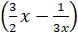 11
11
8. (a) Prove that 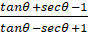 =tan
=tan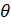 +sec
+sec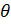
(b) Prove that Cos 20° Cos40° Cos60° Cos80°=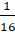
9. (a) One side of a triangular garden is 30 m. If its two corner angles are 22°  and 112°
and 112°  find the cost of planting the gross at the rate of Rs 5 per square meter
find the cost of planting the gross at the rate of Rs 5 per square meter
(b) Prove that 2 tan-1  + tan-1
+ tan-1  =-1
=-1 
DHERA GHAZI KHAN Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes Group-2
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- If n is a prime number then
 is equal to:
is equal to:
(A)Rational
(B)Irrational
(C)Prime Number
(D)Complex number
- {
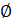 } is equal to:
} is equal to:
(A)Empty set
(B)Singleton set
(C)Rational set
(D)Solution set
- If A is a square matrix of order 2 x 2 then IKAI is equal to:
(A)K2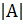
(B)K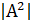
(C)K2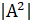
(D)K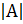
- The cofactors of an element aij denoted by Aij equals:
(A)(-1)i+j Mij
(B) (-1)i-j Mi+j
(C) (-1)i-j Mij
(D) (-1)ij Mi+j
- If 43x=
 then X equals:
then X equals:
(A) 
(B) 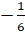
(C) 6
(0) -6
- For ax2 + bx +c =0 , if b2 -4 ac <0 then roots are :
(A) Rational
(B) Equal
(C)Real
(D) Imaginary
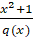 + will be proper fraction if degree of q(x) equals:
+ will be proper fraction if degree of q(x) equals:
(A) 1
(B) 2
(C) 3
(D) 0
- Reciprocals terms of Harmonic sequence equals:
(A) A.P
(B) H.P
(C)G.P
(D) Arithmetic series
-
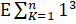 equals:
equals:
(A) 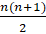
(B) 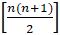 2
2
(C) 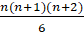
(D) 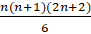
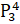 equals:
equals:
(A) 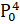
(B) 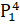
(C) 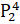
(D)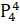
- For an element A the range of its probability equals:
(A) 0 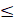 P (A)
P (A)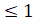
(B) 0 <P(A) <1
(C) -1<P(A) <1
(D)-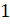
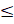 P (A)
P (A)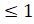
- For an element A the range of its probability equals:
(A)2n + I
(B) 2n
(C) n
(D)n + I
- The inequality n! > 2n+1 is valid if:
(A) n<4
(B) n  4
4
(C) n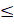 3
3
(D)n = 3
- The area of sector of circular region of radius r equals:
(A)2 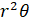
(B) 
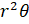
(C) 
(D) 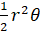
- 2 Cos2
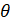 /2 equals:
/2 equals:
(A)1+Cos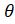
(B)1 -Cos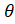
(C)1-Sin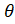
(D)I + Sin 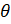
- The domain of sins equals:
(A) [-1,1]
(B) 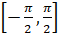
(C) 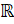
(D)Q
- With usual notation the value of a+b-c equals:
(A) 2(s-c)
(B)2(s-b)
(C)2(s-a)
(D) 2s
- e-radius corresponding to < B equals:
(A) 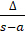
(B) 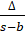
(C) 
(D) 
- Cos (sin-1
 ) equals:
) equals:
(A) 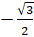
(B) 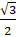
(C) 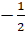
(D) 
- If sin x=
 then x equals, x
then x equals, x 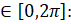
(A) 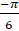
(B) 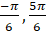
(C) 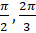
(D) 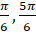
DHERA GHAZI KHAN Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
(Subjective Type)
Time Allowed: 2:30 Hours Group-II
Maximum Marks: 80
NOTE:- Write same question number and its part number on answer book, as given in the question paper.
SECTION-I
2. Attempt any eight parts.
- Prove that
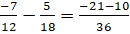
- Factorize a2 + 4b2
- Simplify (5,-4) (-3,-2)
- Define a sermi — group
- Write the inverse and contra positive of the conditional
 P
P q
q
- Find any two proper subsets of a set {a, b, c}
- If the matrix
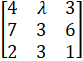 is singular, then find the values of
is singular, then find the values of 
- If A =
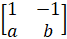 and A2 =
and A2 =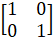 Find the values of a and b
Find the values of a and b
- For the matrices
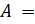
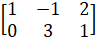 and A2 =
and A2 =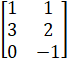 , evaluate BtAt
, evaluate BtAt
- Prove that

- Use synthetic division to show that 2 and — 3 are the solutions of the polynomial equation 2x4+ 7x3 — 4,0 — 27x — 18
- If
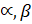 are the roots of 3x2 — 2x + 4 = 0. Find the value of
are the roots of 3x2 — 2x + 4 = 0. Find the value of 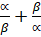
3. Attempt any eight parts.
- Define the term conditional equation with example
- If an— 3 = 2n — 5. Find nth term of sequence.
- How any terms of series —7 + (-5) + (-3) +……………amount to 65
- Find the G.Ms between —2
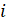 and 8
and 8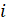
- If
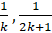 and
and 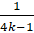 and in H.P. Find k
and in H.P. Find k
- How many signals can be given by 5 flags different colors using 3 flags at a time.
- Find the value of n, when nC10=
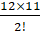
- How many necklaces can be made from 6 beads of different colors?
- If sample space S = {1,2,3,4……….9} and A= {2,4,6,8} B = {1, 3, 5), Find P(AUB)
- State Binomial theorem for positive Intigral Index N
- Show that
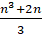 represents an Intigral for n = 1.2
represents an Intigral for n = 1.2
- Expand (I — 2x)1/3 up to 4 terms.
4. Attempt any six parts.
- Find
 , if
, if  = 65°20', r = 18 mm
= 65°20', r = 18 mm
- Find x, if Tan245° —Cos2 60° = x Sin 45° Cos 45° Tan60°
- Prove Cos2
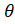 Sin2
Sin2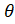 =
=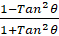
- Prove
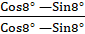 — Tan 37°
— Tan 37°
- Prove 1 + Tan
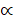 ,Tan 2
,Tan 2 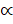 = Sec2
= Sec2 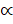
- Prove
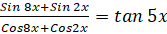
- Find the period of 3 Cos

- In
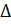 ABC, b = 125,
ABC, b = 125, 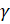 = 53°.
= 53°. 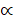 = 47°. Find
= 47°. Find 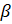 and C
and C
- The area of triangle is 2437. If a = 79.C= 97. Find
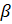
- Prove r3 = S Tan

- Prove cos (Sin-1 x) =
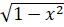
- Solve Tan2
 =
=
- Solve secx = -2,x
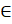 [0, 2
[0, 2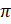 ]
]
SECTION-II
NOTE: - Attempt any three questions.
5. (a) Convert (A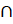 B)' = A'UB' to Logical form and prove by constructing truth table.
B)' = A'UB' to Logical form and prove by constructing truth table.
(b) Verify that (AB)-1 =B-1 A-1 if 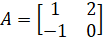 B =
B = 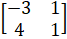
6. (a) Solve (x+1) (x+2) (x+3)(x+4)= 24
(b) Resolve into partial fractions of, 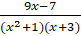
7. (a) Find the sum of 20 terms of the series whose rth term is 3r+ 1
(b) Find the term independent of x in the following 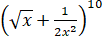
8. (a)Prove the identity 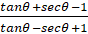 tan =
tan =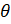 +sec
+sec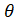
(b) Prove that Cos20° + Cos 100° + Cos 140°= 0
9. (a) Solve using first law of tangents and then law of sines b = 61 , a = 32 , 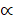 = 59° 30
= 59° 30
(b) Prove that tan-1 + tan-1
+ tan-1 — tan-1
— tan-1 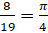
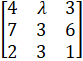
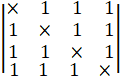 = (x + 3)(x -1)3
= (x + 3)(x -1)3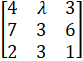 is singular, then find the values of
is singular, then find the values of 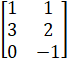 , evaluate BtAt
, evaluate BtAt