Federal Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- Reference angle lies in quadrant:
- IV
- I
- II
- III
- The set {0, 1} is closed w.r.t:
- Division
- Addition
- Subtraction
- Multiplication
-
 belongs to the set of:
belongs to the set of:
- Rational Numbers
- Real Numbers
- Complex Numbers
- Integers
- The set of integers Z is a group under:
- Addition
- Subtraction
- Division
- Multiplication
A declarative statement which may be true or false but not both is called:
- Tautology
- Proposition
- Deduction
- induction
- If
 and A is singular matrix,
and A is singular matrix,
then x =
- 3
- 0
- 1
- 2
- The product of all fourth roots of unity is:
- 2
- 1
- 0
- -1
- A fraction in which the degree of numerator is less than the degree of the denominator is called:
- Algebraic Relation
- improper Fraction
- Proper Fraction
- Equation
- 13 + 23 + 33+…….
 3 =
3 =




- An infinite Geometric series converges only if:


-
 > 1
> 1
 < 1
< 1
- An event E is said to be sure if
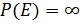


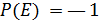
- Numbers of terms in the expansion of (a + b)n is:
- n2+1
- n+1
-

-
- The sum of odd coefficients in the expansion of (1 + x)n is:
- 2n+1
- n2
- 2n
- 2n-1
- tan
 -=
-=
- —cotθ
- tanθ
- —tan θ
- cotθ
- If cotθ < 0 and if cotθ > 0, then the terminal arm of angle lies in the quadrant:




-
 =
=
- A 4sinα-3sin3α
- B 4cos3α+3cosα
- C 3cos3α-4cosα
- D 3sinα-4sin3α
- The period of
 is:
is:
-

-

-

-

- The range of
 is:
is:
- R-


- R+
- A circle that passing through the vertices of a triangle is called:
- Inscribed circle
- Circumed circle
- Escribed circle
- None of above
Federal Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 2.10 Hours
MAXIMUM MARKS: 60
SUBJECTIVE
1. Attempt any Eight of the following. All carry equal marks.
SECTION-I
- Simplify by using De Moivre's Theore

- Give logical prove of the theorem
 '=
'= '
' '
'
- Without expansion verify that
 0
0
- Fine the values of a and b if -2 and 2 are the roots of The polynomial x3 -4x2+ax+b
- Resolve into partial fractions
 .
.
- Insert four harmonic means between
 -11
-11
and 
- Find values of n and r1 when
 :
: :
:
- Show that the middle term of
 2n is
2n is 
 n
n n.
n.
- Prove that

- Without using table or calculator, prove that sin 19° cos11° + sin71° sin11°=

- Find the period of cosine function.
- The sides of triangle are x2+x+1, 2x + 1 and x2 - 1. Prove that the greatest angle of the triangle is 1200.
- Show that cos-1
 =
= - cos-1
- cos-1 
- Solve


SECTION — C
(Marks 40)
Note: Attempt any FIVE questions. All questions carry equal marks: (5x8=40),
Q3. Use matrices to solve the following system:
Q4. Show that the roots of equation
 are real. Also shoW that the roots will be equal only if
are real. Also shoW that the roots will be equal only if 
Q5. -Show that sum of n A.Ms between a and b is equal to n times their A.M.
Q6.Expand  up to 4 terms.
up to 4 terms.
Q7.Prove that: sin  sin
sin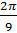 sin
sin sin
sin =
=
Q8.Prove that in an equilateral triangle,  1
1 
Q9.Solve the equation  =
= +
+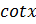
 0
0
![]() are real. Also shoW that the roots will be equal only if
are real. Also shoW that the roots will be equal only if ![]()
![]() up to 4 terms.
up to 4 terms.![]() sin
sin![]() sin
sin![]() sin
sin![]() =
=![]()
![]() 1
1 ![]()
![]() =
=![]() +
+![]()