Federal Board 2017
INTERMEDIATE PART-II (12th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE   
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.

Q.No.1

• What equal   =+2, and =:

A. 0
B. -64
C. 24
D. 28

• Which of the following is a unit vector in the direction of [2,6] ?

A.
B.
C.
D.

• What is the value of -1 (6) ?

A.
B. 31
C. -1
D. 1

• What is the value of g  if =  and?

A.
B.
C.   
D.

• If  then which of the following options is correct?

A.        
B.
C.      
D.

• Which of the following defines a function?

A.  
B.
C. 2  
D.

• If 2  then which of the following option is correct?

A. 0         
B. 1         
C. -2       
D. -1

• Which of the following represents = y?

A.  
B.
C.
D.

• What evaluates?

A.        
B. 0         
C. -       
D.

• For what value of k,  =30

A. 5         
B. -5
C. -35
D. 0

• If   and  then what results  ?

A. 0         
B. 4
C. 2         
D. 8

• What is the area under the curve  from  ?

A. 1         
B. 2
C.         
D. 0

• What is the perpendicular distance of the line  from origin?

A. 5         
b. 1         
C. 0         
D.

• Which of the following is an equation of line passing through (1,0) and (0,1) ?

A.  
B.
C.
D.

• For what value of  lines  and are parallel?

A. -2       
B. 2         
C. 0         
D. 1

• Which of the following ordered pairs does not satisfy

A. (0,0)  
B. (3,0)
C. (1, 1) 
D. (-2, 1)

• What is the length of the Latus Rectum of the parabola 2

A. 16      
B. 8
C.          
D. 4

• Which of the following ordered pairs ' describes x-intercept of the conic
  2

A. (-3, 0)
B. (0,3+ )
C. (3, 0) 
D. (0, 3)

• Which of the following is an axis of the parabola 2

A.           
B. 
C. x = -
D. x =

• For what value of  , vectors 5 - +  and  + 3 - 3 are parallel to each other?

A. 3         
B. -3
C. -15
D. +15

Federal Board 2017
INTERMEDIATE PART-II (12th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 2.10 Hours
MAXIMUM MARKS: 60
SUBJECTIVE
SECTION-I

2. Attempt any Eight of the following. All carry equal marks.

• Let the real valued functions  and  be defined by and2-
  
• Obtain the expressions for22
  
• Evaluate
  
• Find  If = and
  
• Differentiate   with respect to  by ab-initio method.
  
• A box with a square base and open top is to have a volume of 4 cubic dm. Find the dimensions of the box which will require the least material?
  
• Show that  = sin-1
  
• Evaluate  
  
• A quadrilateral has the points A (9 , 3) , l3(-7 , 7), C(-3, -7) and D (5, - 5) as. its vertices. Find the midpoints of its sides. Show that the figure formed by joining the mid points consecutively is a parallelogram.
  
• Find equation of two parallel lines perpendicular to such that the product of the andintercepts of each is 3.
  
• Find the equations of two tangents drawn from (2,3)to the circle 22 =9.
  
• Find the foci, eccentricity and vertices of an ellipse  
  
• Find the equation of tangents to the conic 22 and parallel to the
  
• Find the angle between the vectors  ,and+
  
• Use vector method to prove that sin ( —) = sin  cos — cos  sin

SECTION - C

Note: Attempt any FIVE parts. All questions carry equal marks.
Q.3     If  = 
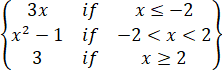
Discuss continuity at  and

Q.4     Find the extreme values of the function occurring in the interval [0, 2

Q.5     Evaluate  

Q.6     Show that the lines and  are concurrent and the third-line bisects the angle formed by the first two lines.

Q.7     Graph the feasible region of the system of linear inequalities


and find the corner points.

Q.8     Find the equation of circle passing through the points A (1, 4) B (-1, 8) and tangent to the line

Q.9     Prove that the altitudes of a triangle are concurrent.