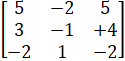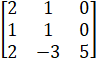Gujranwala Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- If Z is a complex number then
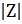 2 equals:
2 equals:
(A)Z2
(B)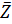 2
2
(C) 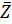
(D) Z
- For a set A and universal net U. then A U .Ac equals:
(A) U
(B) Ac
(C)A
(D) 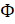
- If B=
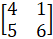 then cofactor of 5 equals:
then cofactor of 5 equals:
(A)1
(B) —1
(C) 4
(D)6
- Transpose of a diagonal matrix equals:
(A) Null matrix
(B)Row matrix
(C)Diagonal matrix
(D)Column matrix
- Nature of roots of quadratic equation can be found with the help of
(A) Discriminant
(B) Factor theorem
(C)Long division
(D) Remainder
- The product of four-fourth roots of unity equals:
(A)0
(B) 2
(C) 1
(D) —1
- Partial fractions of
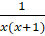 equals.
equals.
(A) 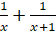
(B) 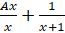
(C)  +
+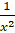
(D)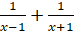
- Harmonic mean between
 and
and  equals:
equals:
(A) 
(B) 
(C) 
(D) 
- Sum of an infinite geometric series exists if:
(A) r =1
(B) 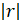 <1
<1
(C) 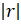 >1
>1
(D) r = —1
- If
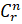 =
=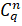 which of the following must be true:
which of the following must be true:
(A)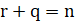
(B) 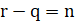
(C) 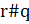
(D) 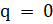
- A coin is tossed once then P(s) is equal to
(A) 
(B) 
(C) 2
(D)1
- The sum of all coefficients in the binomial expansion of (1 + x)n is
(A)2n-1
(B) 2n+1
(C) 2n
(D)0
- 1 -x + x2-x3 +……………………..is expansion equals:
(A)(1 +x)2
(B) (1 -x)2
(C) (1+x)-1
(D) (I —x)-1
- cos (
 — 90°) — cos (
— 90°) — cos (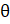 + 90°) equals:
+ 90°) equals:
(A) —2 cos 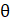
(B) 2cos 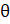
(C) —2 sin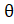
(D) 2 sin 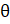
- In two hours the hour hand of a clock turns an angle equals:
(A) 
(B) 
(C) 
(D) 
- The period of 3 tan 3x is equal to:
(A)s 
(B) 
(C) 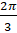
(D) 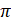
- Area of
 ABC equals:
ABC equals:
(A) 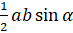
(B) 
(B) 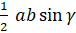
(B) 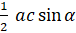
- In an equilateral triangle
 equals:
equals:
(A)1:2:3
(B)1:3:3
(C) 2:3:3
(D)3:3:3
- 2tin-1 A equals:
(A) tan-1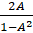
(B) tan-1
(C) tan-1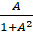
(D) tan-1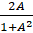
- If sec x = + 2, then x is equal to, x
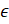 [0,2
[0,2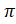 ]
]
(A) 
(B) 
(C) 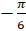
(D) 
Gujranwala Board 2017
INTERMEDIATE PART-I (11th CLASS)
MATHEMATICS (NEW SCHEME)
(COMMERCE GROUP)
TIME ALLOWED: 2.10 Hours
MAXIMUM MARKS: 60
SUBJECTIVE
1. Attempt any Eight of the following. All carry equal marks.
SECTION-I
- Simplify
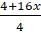 by justifying each step.
by justifying each step.
- Find the multiplicative inverse of the complex number (
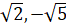 )
)
- Simplify:

- What is the difference between the sets {a, b} and {{a, b}} ?
- Show that the statement
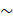 (p
(p q)
q) p
p
- Define monoid group.
- Evaluate the determinant
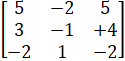
- If A =
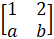 and
and  2=
2= 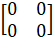 Find the value of a and b.
Find the value of a and b.
- If matrix A is skew-symmetric, then show that A2 is symmetric.
- Find roots of the equation 4x2+7x-1=0
- When the polynomial x3 + 2x2+kx+4 is divided by x-2, the remainder is 14. Find k.
- Show that the roots of the equation x2 -2(
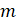 +
+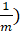 x+3 = 0. m
x+3 = 0. m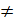 0 will be real.
0 will be real.
3. Attempt any eight parts.
- Define the term identity with example.
- Write the first three terms of sequence if an - an -1 = n +2, a1 = 2
- If
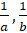 and
and  are in G.P. Show that common ratio is ±
are in G.P. Show that common ratio is ± 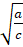
- Find the 9th term of harmonic sequence
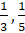 ,
,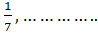
- If a = -2. b = -6. Find A, G.
- How many words can be formed from the letter "PLANE" Using all letters (No. letter is repeated)?
- Prove that
 , =
, =
- Find the number of diagonals of a 6-sided figure.
- A coin is tossed four times. Find the probability that top shows. all heads.
- Show that n3- n is divisible by 6 for n = 2.3
- Evaluate ( 1.03)1/3 by binomial theorem up to three places of decimals.
- Find the middle term of (a + x)? When n is even.
4. Attempt any six parts.
- Express in radian 120'40"
- Verify 2 sin 45° +
 cosec 45° =
cosec 45° =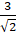
- Prove cosec
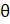 + tan
+ tan 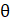 sec
sec 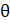 = cosec
= cosec 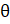 sec2
sec2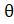
- Without using table or calculator, Find tan (1110o)
- Prove sin (
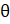 +
+ )=cos
)=cos 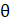
- Prove cos 2
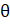 —
—
- Find the period of tan 4 x.
- In
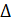 ABC,
ABC,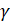 = 90° ,
= 90° ,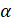 = 62° 40', b= 796, Find
= 62° 40', b= 796, Find 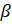 and a
and a
- Find the area of
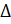 ABC, If a = 18, b =24, c = 30
ABC, If a = 18, b =24, c = 30
- Prove
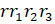 =
= 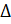 2
2
- Prove cos-1 (—x) =
 — cos-1x.
— cos-1x.
- Solve cot
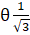 ,
, [0,2
[0,2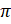 ]
]
- Solve cosec2
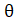 =
=
SECTION-II
NOTE: - Attempt any three questions.
5. (a) Prove that A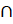 (B
(B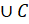 ) = (A
) = (A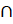 B)
B)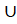 (A
(A C)
C)
(b) Find the inverse of 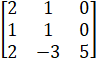
6. (a) Solve the following system of equations: 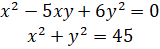
(b) Resolve the following into partial fractions: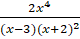
7.(a) If y = 1 + 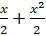 ……………Show that x= 2
……………Show that x= 2 
(b) Find the term independent of x in the following expansion: 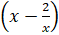 10
10
8. (a) Prove that (tan  + cot
+ cot 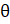 )2= sec2
)2= sec2 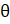 cosec2
cosec2 
(b) Prove that sin 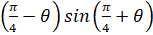 =
=  cosec2
cosec2 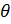
9. (a) Prove that 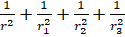 =
=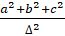
(b) Prove that sin-1 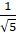 +cot -1 3=
+cot -1 3=