(A) 2sinx
(B) 2 cos x
(C) 0
(D) -2 cos x
![]() is equal to:
is equal to:
(A) ![]() na
na
(B) 0
(C) 1
(D) α
Gujranwala Board 2017
INTERMEDIATE (12th CLASS)
PART-II
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
(A) 2sinx
(B) 2 cos x
(C) 0
(D) -2 cos x
is equal to:
(A)
na
(B) 0
(C) 1
(D) α
(A) 9(x³ + 1)8
(B) 27x² (x³+ 1)9
(C) 3x² (x³ + 1)8
(D) 27x² (x³+ 1)8
(A) f’(x)
(B) f(x)
(C) f’(x)
(D) f’(a)
(A) sec² x
(B) tan² x
(C)
(D) tan x sec x
(A)
(B)
(C)
(D)
(A) af(x) f’(x)
(B) af(x) f’(x).a
(C) af(x) f’(x)na
(A) 2
+ c
(B) -2
(C)+c
(D)+c
(A)
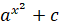
(B)
(C)+ c
(D)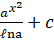
(A)
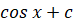
(B)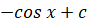
(C)+c
(D)+c
(A)
+ c
(B) -+ c
(C)+ c
(D)+c
(A) -1
(B) 0
(C) 1
(D) 90°
(A) 2:1
(B) 1:2
(C) 2:3
(D) 1:1
(A) a1b2+ a2b1 = 0
(B) a1a2 - b1b2 = 0
(C) a1a2 + b1b2 = 0
(D) a1b2 = a2b2
(A) centroid
(B) orthocenter
(C) e-center
(D) circumcentre
(A) solution
(B) optimal solution
(C) minimum solution
(D) maximum solution
(A) foci
(B) vertices
(C) covertices
(D) centre
(A) circle
(B) ellipse
(C) parabola
(D) hyperbola
(A)
,

(B)
(C)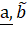
(D),
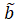
(A) ab
(B) ab cos
(C) ab sin
(D) —ab
Gujranwala Board 2017
INTERMEDIATE PART-I (12th CLASS)
MATHEMATICS (NEW SCHEME)
(COMMERCE GROUP)
TIME ALLOWED: 2.10 Hours
MAXIMUM MARKS: 60
SUBJECTIVE
SECTION-I
1. Attempt any Eight of the following. All carry equal marks.
3. Write short answers to any Eight questions.
4. Write short answers to any Nine questions.
SECTION-II
NOTE: - Attempt any three questions.
5. (a). Prove that ![]()
(b). Find ![]() Ifx=
Ifx=![]() +
+![]() -, y=
-, y=![]() +1
+1
6. (a). Evaluate ![]()
(b). Find the point three-fifth of the way along the line segment from A(-5, 8) to 6(5, 3).
7. (a). Evaluate ![]()
(b). Find the minimum and maximum value of f(x , y) = 4x+ 5y under the constraints 2x -3y ![]() 6 2x + y
6 2x + y![]() 2 2x + 3y
2 2x + 3y![]() 12 x
12 x![]() 0, y
0, y![]() 0
0
8. (a).Find length of tangent from point P(x1,y1) to circle x2 + y2 + 2gx + 2fy + c = 0
(b) By vector method, prove that angle inscribed in a semi-circle is right angle.
9. (a). Find an equation of the hyperbola with foci (5 , -2), (5 , 4) and one vertex (5, 3).
(b). Prove by vector method: sin (![]() )= sin
)= sin ![]() cos
cos ![]() + cos
+ cos ![]() sin
sin![]()