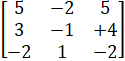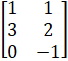LAHORE BOARD 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes Group-1
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- The roots of equations x2 + 5x + 6 = 0 are:
(A) 2,-3
(B) -2,-3
(C) 2,3
(D) -2,3
- The sum of odd coefficient in the expansion of (1 + x)5 is:
(A) 5
(B) 16
(C) 25
(D) 32
- A Quadratic equation has degree:
(A) 0
(B) 1
(C) 2
(D) 3
- nCr is equal to:
(A) 
(B)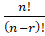
(C) 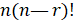
(D) 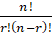
- If z = 3 — 4i then is|
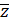 |---------------:
|---------------:
(A) 4
(B) 5
(C) —5
(D) 1
- Arithmetic mean between
 is:
is:
(A)
(B)
(C) 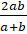
(D) 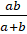
 equals:
equals:
(A) 
(B) 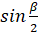
(C) 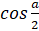
(D) 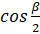
- cos-1
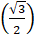
(A) 
(B)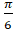
(C) 
(D)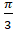
- Period of
 is:
is:
(A) 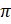
(B) 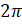
(C) 
(D)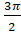
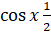 .has solution-------------
.has solution------------- 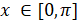
(A) 
(B) 
(C) 
(D) 
- Harmonic mean between 3 and 7 is
(A) 
(B) 
(C) 5
(D) 21
- The value of cos 315° is:
(A) 0
(B) 1
(C) 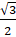
(D) 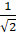
- Notation for radius of in-circle is:
(A) r
(B) R
(C) r1
(D) 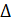
- Number of terms in the expansion of (1 + x)2n+1 is:
(A) 2n + 1
(B) 2n
(C) 2n + 2
(D) 3n + 1
- If
 = 0 then k = - - - :
= 0 then k = - - - :
(A) 16
(B) 0
(C) +4
(D) 8
- Partial fractions of
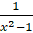 will be of the form:
will be of the form:
(A) 
(B) 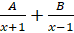
(C) 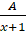
(D) 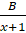
- If A is a matrix of order 3 x 4 then order of AA' is:
(A) 4 x 3
(B) 3 x 4
(C) 4 x 4
(D) 3 x 3
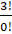 equals:
equals:
(A) 3
(B) 6
(C) 
(D) 12
 rotation (anticlockwise) =:
rotation (anticlockwise) =:
(A) 45°
(B) 90°
(C) 188°
(D) 360°- Set integers is a group with respect to:
(A) +
(B) ÷
(C) X
(D) -
LAHORE BOARD 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
(Subjective Type)
Time Allowed: 2:30 Hours
Group-1
Maximum Marks: 80
NOTE:- Write same question number and its part number on answer book. As given in the question paper.
SECTION-I
2. Attempt any eight parts.
- Does the set { 0, — I} possess closure property with respect to:
(a) addition
(b) multiplication
- Find multiplicative inverse of
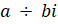
- Prove that I z1 z2 I = I z1 I I z2 I
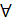 z1, z2
z1, z2 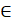 C
C
- Define proper subset and improper subset.
- Show that the statement is tautology ͠
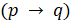
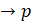
- If
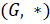 is a group with ‘e’ its identity then ‘e' is unique?
is a group with ‘e’ its identity then ‘e' is unique?
- A =
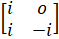 , show that A4 = I2
, show that A4 = I2
- A =
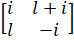 show that A — (
show that A — (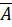 ) is skew-hermitian.
) is skew-hermitian.
- Without expansion how that
 =0
=0
- Solve the equation

- When x3 + kkx2 — 7x + 6 is divided by x + 2 the remainder is —4? Find the value of k.
- Prove that the 1 +
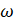 +
+ 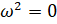
3. Attempt any eight parts.
- Resolve
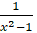 into partial fractions.
into partial fractions.
- If
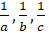 are in G.P. show that r,= +
are in G.P. show that r,= + 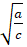
- Convert recurring decimal 0.7 into vulgar fraction.
- If 5 is the harmonic mean between 2 and b, find b?
- Find the A.P whose nth term is 3n — 1.
- How many words can be formed from the letters of the word 'Objective" using all letters without repeating any one?
- In how many ways 4 keys can be arranged on a circular key ring
- Find the values of n and r when nCr = 35 and nPr = 210
- If S ={ 1.2, 3, ----- 9 }, Even A = { 2. 4. 6. 8} B = { 1, 3, 5}, find P ( A U B )
- Prove that 1 + 5 + 9 + = (4n —3) = n (2n — 1), for n = 1 and n = 2
- Expand upto three terms
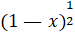
- Using binomial therem, calculate (0.97)3
LAHORE BOARD 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
Group-2MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- One root of the equation x2- 3x + a = 0 is 2, then a is:
(A) -2
(B) 2
(C) 3
(D) -3
- The number of terms in the expansion of (x2-1)7 is:
(A) 2
(B) 7
(C) 8
(D) 12
- A quadratic equation has degree:
(A) One
(B) Two
(C) Three
(D) Four
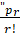 is equal to:
is equal to:
(A) nCr
(B) nCr-1
(C) n+1Cr
(D) n-1Cr
- |a + bi l is equal to:
(A) 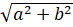
(B) 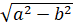
(C) 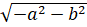
(D) 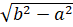
- Geometric mean between 4 and 16 is:
(A) ÷4
(B) ÷8
(C) ÷16
(D) ÷64
- Radius of escribed circle opposite to vertex A is equal to:
(A)
(B) 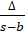
(C)
(D) 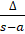
- cos(sec-11) is equal to:
(A) 1
(B) 0
(C) 30o
(D) 2 <
- The domain of
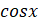 is:
is:
(A) [0. 1]
(B) 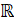
(C) [-1, 1]
(D) [ -1, 0]
- An equation containing at least one trigonometric function is called:
(A) Algebraic equation
(B) Quadratic equation
(C) Linear equation
(D) Trigonometric equation
- if the nth term of an A.P is
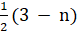 then first three scents are:
then first three scents are:
(A) 3,2, 1
(B) 1, 2, 3
(C) 1,2,1
(D) 1, 
- Tan
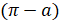 equal to:
equal to:
(A) 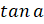
(B) 
(C) 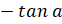
(D) 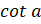
- The point of intersection of the angular bisectors of a triangle is called:
(A) Circum centre
(B) Orthocentre
(C) In-centre
(D) Centroid
- The expansion of (1 + 2x)-1 is valid if:
(A) 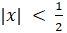
(B) 
(C) 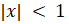
(D) 
- If A and B are matrices then (AB)t is equal to:
(A) Bt. At
(B) At. Bt
(C) AB
(D) BA
- The fraction

(A) Improper
(B) Proper
(C) Equivalent
(D) Identity
- The inverse of a square matrix exists if A is:
(A) Singular
(B) Non-singular
(C) Symmetric
(D) Rectangular
- nCo is equal to:
(A) nP2
(B) nCn
(C) nC2
(D) nCn+1
 is equal to:
is equal to:
(A) 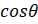
(B) tan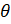
(C) 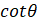
(D) 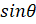
- If a function f:
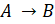 is such that Range
is such that Range 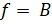 then
then 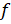 is called:
is called:
(A) Injective
(B) Surjective
(C) Into
(D) Periodic
LAHORE BOARD 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
(Subjective Type)
Time Allowed: 2:30 Hours
Group-IIMaximum Marks: 80
NOTE:- Write same question number and its part number on answer book, as given in the question paper.
SECTION-I
2. Attempt any eight parts.
- Prove that
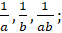 justify each step.
justify each step.
- Factorize: +
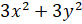
- Simplify:
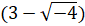 -3
-3
- Write power set of {9, 11}
- Define implication or conditional.
- Write tte inverse of {1, 3), (2, 5), (3, 7), (4,9), (5, 11)}
- If A =
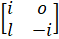 , then find A2
, then find A2
- Find inverse of
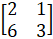
- If B =
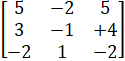
- Solve
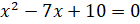
- Prove that
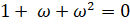
- The sum of a positive number and its reciprocal is
 . Find the number.
. Find the number.
3. Attempt any eight parts.
- Define proper rational fraction.
- Which term of the arithmetic sequence 5, 2, —1, ----- is — 85?
- Find the next two terms of sequence —I, 2, 12, 40,------------
- Show that the reciprocals of teens of geometric sequence a1, a1r2, a1r4, ---- form another geometric sequence.
- First term of harmonic sequence is
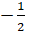 and fifth terms is
and fifth terms is  . Find 9th term.
. Find 9th term.
- Find the value of when 11Pn = 11.10.9
- Find the value of n and r when nCr= 35 and nPr = 210
- A coin is tossed four times. Find probability of the events happening 2 heads and 2 tails.
- A die is thrown. Find probability that the dots on the top are prime numbers or odd numbers.
- Use mathematical induction to prove that 1+
 +
+  + ---+
+ ---+ 
for n = 1,2
- Show that
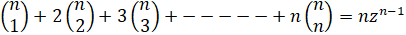
- Expand
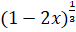 up to three terms.
up to three terms.
4. Attempt any six parts.
- Find
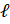 , when
, when 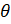 = 65° 20’, r= 18mm
= 65° 20’, r= 18mm
- If tan2 45° — cos2 60° = xsin45° cos45° tan60° then find x
- Prove that
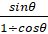 + cot
+ cot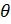 = cosec
= cosec 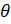
- if
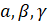 are the angles of a
are the angles of a 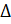 ABC, then prove that cos
ABC, then prove that cos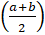 =sin
=sin
- Prove that sin
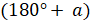

- Prove that sin
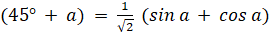
- Find the period of
 .
.
- At the top of a cliff 80m high, the angle of depression of a boat is 12°. How far is the boat from the cliff?
- Solve the
 ABC in which
ABC in which 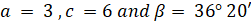
- Find the smallest angle of the
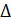 ABC, when
ABC, when 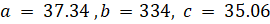
- Without using calculator. show that cos-1
 .
.
- Solve the equation
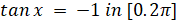
SECTION-II
NOTE: - Attempt any three questions.
5. (a) For any three sets A, B and C, prove that A (BUC) = (AUB) U (A
(BUC) = (AUB) U (A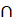 C)
C)
(b) Verify that (AB)t =Bt At if 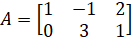 and B =
and B = 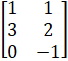
6. (a) Solve 32x-1 – 12.3x +81 = 0
(b) Resolve into partial fractions of, 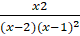
7. (a)If  the prove that
the prove that 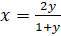
(b) Use the mathematical induction to prove that 1+4+7+----+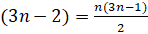
8. (a) Show that 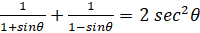 f
f
(b) Prove that 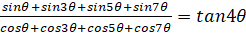
9. (a) Show that 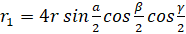
(b) Prove that tan-1 + tan-1
+ tan-1 — tan-1
— tan-1 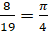
 =0
=0