(a) ex - e-x
(b) ex + e-x
(c) ![]()
(d) ![]()
Lahore Board 2017
MATHEMATICS-II
Inter (Part-II) 2017
Mathematics
Group-I
PAPER: II
Time: 30 Minutes
(OBJECTIVE TYPE)
Marks: 20
Note: Four possible answers, A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink in the answer-book. Cutting or filling two or more circles will result in zero mark in that question.
(a) ex - e-x
(b) ex + e-x
(c)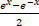
(d)
(a) 0
(b) 1
(c)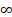
(d) 2
(a) 4 cot 2x cosec 2x
(b) -4 cot 2x cosec² 2x
(c) 4 cot² 2x cosec 2x
(d) -4 cot 2x
(a)
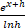
(b)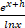
(c) ex+h
(d) hex+h
(a) 1
(b) 0
(c)
(d) -1
(a) 1 -
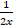
(b)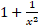
(c) 0
(d)
(a) 2(x² + 1)
(b)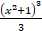
(c) 2x(x² + 1)
(d) 4x(x² + 1)
(a)
n (x + 2) + c
(b) x + 2n (x + 2) + c
(c) x - 2n (x + 2) + c
(d) x -n (x + 2) + c
(a) ex.
+ c
(b)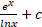
(c)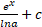
(d) exx+c
(a) 0
(b)
(c)
(d)
(a) sec x tan x + c
(b) sect x tan x + c km
(c)n (sec x - tan x) + c
(d)n (sec x + tan x) + c
(a) h² - ab = 0
(b) h² + ab = 0
(c) a+b=0
(d) a-b=0
(a) m1n2 = 0
(b) m1n2 + 1 = 0 V
(c) m1n2 - 1 =0
(d) m1 + n2 = 0
(a) 0
(b) 2
(c)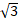
(d)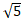
(a) 1 point V
(b) 0 point
(c)points
(d) 2 points
(a) 9x + 2y < 8
(b) - x + 3y < 0
(c) 3x + 5y < 6
(d) 3x + 5y > 4
(a) Circle
(b) Parabola
(c) Ellipse
(d) Hyperbola
(a)
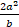
(b)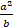
(c)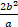
(d)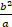
(a) Right angle
(b) Obtuse angle
(c) Reflexive angle
(d) 0°
(a) 0
(b) 2
(c) 1
(d) 4
MATHEMATICS-II
Inter (Part-II) 2017
Mathematics
Group-I
PAPER: II
Time:2: 30 Hours
Marks: 80
(SUBJECTIVE TYPE)
3. Write short answer to any EIGHT(8) questions
4. Write short answer to any NINE (9) questions
Note: Attempt any THREE(3)questions
Q.5(a) Find ![]()
(b) Find ![]() if x=a (cos t + sin t), y=a(sin t – t cos t)
if x=a (cos t + sin t), y=a(sin t – t cos t)
Q.6 (a) Evaluate ![]()
(b) The vertices of a triangle are A(-2,3),B(-4,1),C(3,5), find the centre of the Circumcircle of the triangle
Q.7 (a) Find area between x-axis and curve y =![]()
(b) Minimize f(x,y) = x+3y subject to constraints 2x+5y<30, 5x+4y<20 x>0,y>0
Q.8(a) Show that the line 3x-2y=0 and 2x+3y-13=0 are tangents to the circle x2+y2+6x-4y=0
(b) Prove that in any triangle ABC b=c cos A + a cos C by using vectors
Q.9 (a) Find the point of intersection of ![]()
(b) Fsind the vaues of (i) ![]() (ii)
(ii) ![]()
MATHEMATICS-II
Inter (Part-II)
Mathematics 2017
Group-II
PAPER: II
Time: 30 Minutes
(OBJECTIVE TYPE)
Marks: 20
Note: Four possible answers, A, B, C and D to each question are given. The choice which you think is correct, fill that circle in front of that question with Marker or Pen ink in the answer-book. Cutting or filling two or more circles will result in zero mark in that question.
(a) Ellipse
(b) Circle
(c) Parabola
(d) Hyperbola
(a) e1/5
(b) e5
(c) e-5
(d) e-1/5
(a) 0
(b) 1
(c)
(d) 22
(a)
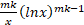
(b)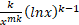
(c)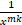
(d)
(a)
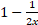
(b)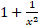
(c) 0
(d)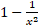
(a) cos x
(b) -cot x
(c) -tan x
(d) -cosec x
(a) Maclaurin's series
(b) Taylor series
(c) Power series
(d) Binomial series
(a) ln cot x + c
(b) ln cos x + c
(c) ln sin x +c
(d) ln sec x +c
(a) ex tan x + c
(c)+ c
(b) ex sin x + C
(d) ex tan-1 x + c
(a)

(b)
(c)
(d)
(a) y = e²x
(b) y ce-x
(c) y = ex
(d) cex
(a) y=a
(b) y = b
(c) x = a
(d) x = b
(a) a1 a2 = 0
(b) a1 - b1 =
(c) a1b1 - a2b2 = 0
(d) a1b2 a2b1 = 0
(a) 30v
(b) 60°
(c) 45°
(d) 180°
(a)
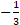
(b)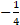
(c)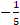
(d) 0
(a) Linear inequality
(b) Identity
(c) Equation
(d) Not inequality
(a) π
(b) 2π
(c) 4π
(d) 8π
(a) x + 2= 0
(b) x-2=0
(c) y +2= 0
(d) y -2 = 0
(a) 1
(b) 2
(c) 3
(d)4
(a) 1
(b) a
(c) 0
(d) b
MATHEMATICS-II
Inter (Part-II)
Mathematics 2017
Group-II
PAPER: II
Time: 2:30 Hours
(SUBJECTIVE TYPE)
Marks: 80
2. Write short answer to any EIGHT(8) questions
3. Write short answer to any EIGHT(8) questions
4. Write short answer to any NINE(9) questions
Section-II
Note : Attempt any THREE questions
Q.5(a) Prove that ![]()
(b) If y=tan (p tan-1x),show that (1+x2)y1-p(1+y2)=0
Q.6(a) Show that ![]()
(b) find the point three-fifth of the way along the line segment from A(-5,8) to B(5,3)
Q.7(a) Evaluate ![]()
(b)Graph the feasible region subject to the following constrains :
![]()
Q.8(a) find a joint equation to the pair if tangents drawn from(5,0) to the circle x2+y2=9
(b) prove that the angle in a semi-circle is a right angle
Q.9(a) derive equation of hyperbola in standard form
(b) by vector method, prove in any triangle ABC,![]()