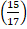Multan Board 2017
Mathematics
PART-I
Time: 30 Minutes
Group 1
Note: Write answers to the questions on the objective answer sheet provided. Four possible answers A, B, C and D to each question are given. Which answer you consider correct, fill the corresponding circle A, B, C and D given in front of each question with Marker or pen ink on the answer sheet provided.
- If nC s = nC12 then nnn equals to:-
- 4
- 8
- 20
- 12
- 2nd term in (1 - x)-1 is:-
- 1
- X
- 2X
- 3X
- If n2>n+3, then it is true for:-
- n = 0
- n< 1
- n
 2
2
- n
 2
2
 tr radian equals to:-
tr radian equals to:-
- 110°
- 130°
- 45o
- 54o
- sin(a-
 ) =____:
) =____:
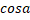
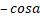


- The period of sin 2x is:-
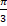
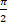
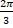
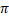
- With usual notations 2s - b =
- a – c
- a + c
- a+2b-c
- a + b
- cos
 =____
=____
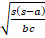

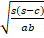



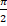
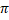
- Cos x=
 , then reference angle is:-
, then reference angle is:-
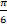

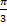

- 1
- -1
- I
- -i
- p
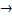 q is called converse of:-
q is called converse of:-
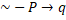
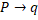
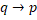
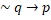
- If A =
 then adj. (A) = ____.
then adj. (A) = ____.

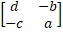
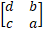
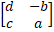
- The rank of the matrix
 is :-
is :-
- Zero
- 1
- 2
- 3
- Four fourth roots of unity are:-
- ±1. ±i
- ±2, ±2i
- ±3, ±i
- ±4, ±4i
- If
 is the complex cube roots of unity, then
is the complex cube roots of unity, then  =________.
=________.

 -1
-1 
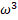
- Partial fractions of
 are of the form:-
are of the form:-
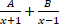
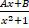
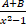

- The fifth term of the sequence an = 2n + 1 is:-
- 7
- 9
- 11
- 13
- Geometric mean between -2i and 8i is:
- ±3
- ±2
- ±1
- ±4
- 5
- 10
- 15
- 20
SUBJECTIVE PART
SECTION B
Q 2. Attempt any eight parts.
- Simplify by justifying each step
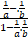
- Simplify (5, -4)
 (-3, -8)
(-3, -8)
- Simplify
 by expressing in the form a + bi.,
by expressing in the form a + bi.,
- Write down power set of the set

- Construct truth table for statement.

- Show that the set N with respect of
 is a semi-group where N is natural number.
is a semi-group where N is natural number.
- Solve the systems of linear equations 3x1
 x2 = 1 and x1 +x2 = 3
x2 = 1 and x1 +x2 = 3
- Without expansion verify that

- Define rank of a matrix.
- If
 is a root of x2+x+1 = 0 show that its other roots is
is a root of x2+x+1 = 0 show that its other roots is .
.
- If
 are roots of ax2 + bx + c = 0, a
are roots of ax2 + bx + c = 0, a  O. Then find the values of
O. Then find the values of 
- Show that roots of the equations px2
 will be rational.
will be rational.
Q 3. Attempt any eight parts.
- Define Partial fractions.
- If
 =
= , b =
, b = then find the arithmetic mean A and the geometric mean G.
then find the arithmetic mean A and the geometric mean G.
- Show that the reciprocals of the terms of G.P, a1, a1r2, a1r4._____form another G.P.
- Find A.M between 1 - x + x2 and 1 +x +x2.
- Write the next term of the sequence I, 6, 20, 56,
- Convert
 in the factorial form.
in the factorial form.
- Prove that n. n-1Pr-1 =NPr.
- A die is rolled. Find the probability of the event when number of dot on the top is less 5.
- Find the value of n when nC10 =

- State Binomial Theorem.
- if x is ,0 small that its square and higher powers can be neglected then show that
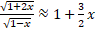
- Expand the varies
 up to 3 terms.
up to 3 terms.
Q 4. Attempt any six parts.
- Find
 when
when  =
= radian, r= 6cm.
radian, r= 6cm.
- Verify
 +
+ =
= 
- Prove the identity

 Sing
Sing Cos
Cos = 1
= 1
- Prove that Sin (180o +a) Sin (90o-a) =-
 .
.
- Show that Sin
 Sin
Sin = Cos
= Cos .
.
- Express
 as product.
as product.
- Find the period of
 .
.
- A vertical pole is Sin-1 high and the length of its shadow is 6m. What is the Angle of Elevation of the Sun at that moment?
- Find the smallest angle of the
 ABC if a=37.34 b = 3.24 c=35.06
ABC if a=37.34 b = 3.24 c=35.06
- In a triangle ABC,
 = 60o,
= 60o, =
=  and b
and b  then find a. c.
then find a. c.
- Show that Sin-1 (-x) =-Sin-1 x
- Solve the equation Sin2 x +
 = 1 when x
= 1 when x 

- Find solution of 4Cos2 x-3 = 0 when x


SECTION-C
NOTE: - Attempt any three questions.
Q 5.
- Consider the set S =
 set up the multiplication table and show S is an abelian group under multiplication.
set up the multiplication table and show S is an abelian group under multiplication.
- Solve the systems of linear equations

Q 6.
- When the polynomial
 2
2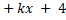 is divided by
is divided by  the remainder is 14. Find the value of k.
the remainder is 14. Find the value of k.
- Resolve
 into Partial Fractions.
into Partial Fractions.
Q 7.
- Insert seven A.Ms between 4 and 8.
- Find the coefficient of xn in the expansion of
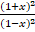
Q 8.
- If
 =
= 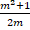 and
and find the values of the remaining trigonometric functions.
find the values of the remaining trigonometric functions.
- Prove the following identity
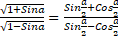
Q 9.
- Prove that in tan equilateral triangle

- Prove that Sin-1
 Sin-1
Sin-1 = Cos-1
= Cos-1