Multan Board 2017
Mathematics
PART-II
Time: 30 Minutes
Note: Write answers to the questions on the objective answer sheet provided. Four possible answers A, B, C and D to each question are given. Which answer you consider correct, fill the corresponding circle A, B, C and D given in front of each question with Marker or pen ink on the answer sheet provided.

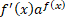

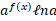
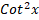
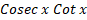
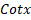
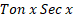
 =:
=:
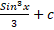
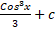
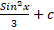
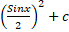
 =:
=:
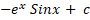
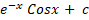
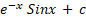
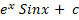
 =:
=:
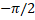
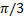
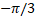
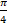
- The degree of the differential equation
 is:
is:
- 1
- 2
- 0
- 3
- A linear equation in two variables represents:
- Circle
- Ellipse
- Parabola
- Straight line
- The slope of the line through the points
 and
and  is:
is:
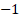
- 0
- 1
- 2
- Slope of a line
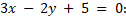

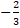

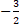
- the perpendicular distance of the line
 from (0, 0) is:
from (0, 0) is:
- 0
- 1
- 2
- 3
 is satisfied by:
is satisfied by:
- (1, 1)
- (1, 2)
- (2, 3)
- (-1, 1)
- The length of the diameter of circle x2 + y2- 6x + 8y = 0 is:
- 4
- 10
- 13
- 12
- The mid point of the line segment joining the foci of an ellipse is called:
- Vertex
- Centre
- Directrix
- Minor axis
- The angle between the vectors
 and
and  is:
is:
-
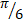
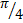
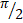

- Projection of
 along
along  is:
is:
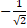
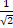
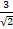

 2at are parametric equations of a:
2at are parametric equations of a:
- Circle
- Ellipse
- Parabola
- Hyperbola
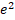
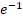
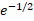
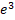
 (where a is constant) is:
(where a is constant) is:


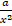
-
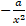
-
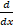
 =:
=:
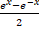

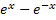
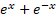
- If
 then y2:
then y2:
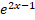
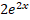
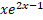
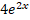
SUBJECTIVE PART
SECTION B
Q 2. Write short answers to any EIGHT parts.
- Define the term Odd and Even function.
- Find Domain and Range of function
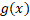 =
=
- Evaluate
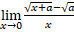
- Differentiate
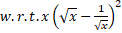
- Find
 if
if .
.
- Find
 if
if  =
=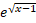
- What is a Stationary Point?
- Differentiate

- Find
 if y – 2xyr + x2y + 3x = O. dx
if y – 2xyr + x2y + 3x = O. dx
- Differentiate
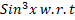
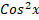
- Find
 If
If 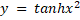
- Find the first two derivatives of Cos (ax + b).
Q 3. Write short answer to any EIGHT parts.
- Using differential find
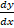 if
if 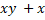 = 4.
= 4.
- Evaluate
 dx.
dx.
- Evaluate
 dx.
dx.
- Evaluate
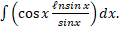
- Find
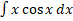
- Evaluate
 dx
dx
- Evaluate
 dx.
dx.
- Solve the differential equation
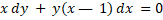 .
.
- Find the area below the curve y=3
 and above the x— axis between x= 1 and x =4
and above the x— axis between x= 1 and x =4
- Evaluate
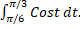
- Define Objective Function.
- Graph the solution region of

Q 4. Write short answer to any SIX parts.
- Find the slope and Inclination of the line joining the points (4, 6), (4, 8).
- Find equation of the line bisecting the first and third quadrants.
- Convert 2x —4y + 11 = 0 in slope intercept form.
- Check whether the lines are concurrent
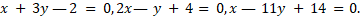
- Find measure of angle of the lines represented by the equation 2x2+ 7xy + 2y2=0.
- Find equation of circle with center (5, -2) and radius 4.
- Find the Directrix of the parabola y2= 80.
- Find equation of ellipse having Foci
 and minor axis of length 10.
and minor axis of length 10.
- Find an equation of hyperbola having Foci
 and e = 2.
and e = 2.
- State Parallel Vectors.
- Find the unit vector in the direction of Vector
 .
.
- Define Vector product of two Vectors.
- Find constant a such that the vectors
 are coplana
are coplana
SECTION - C
Attempt any THREE questions. Each question carries 08 Marks.
Q 5.
- If
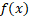 =
= discuss continuity at x = 2.
discuss continuity at x = 2.
- If
 show that
show that 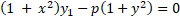
Q 6.
- Evaluate
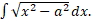
- Find equation of line through the point (2, -9) and Intersection of lines
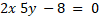 and
and 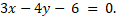
Q 7.
- Evaluate
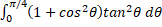
- Minimize
 subject to constraints
subject to constraints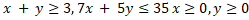
Q 8.
- Find an equation of the parabola whose focus is
 and directrix is
and directrix is 
- Prove that in any triangle ABC b² = c² + a² -2caCosB by Vector Method.
Q 9.
- Find the points of intersection of the conics 3x² + 5y² = 60 and 9x² + y² = 124.
- Find the area of the triangle with vertices
 and
and  by using Vectors.
by using Vectors.
 discuss continuity at x = 2.
discuss continuity at x = 2.