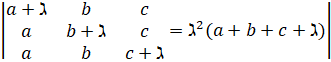Rawalpindi Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
IME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- (z,+) has no identity other than:
(A) 1
(B) -1
(C) i
(D) 0
- (AB)-1 equals:
(A) A-1, B-1
(B) A-1
(C) B-1
(D) B-1, A-1
- |8| is:
(A) Square matrix
(B) unit matrix
(C) scalar matrix
(D) rectangular matrix
- Partial fractions of
 will be of the form:
will be of the form:
(A) 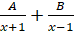
(B) 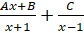
(C) 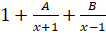
(D) 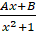
- G.M between 2i and 8i equals:
(A) + 4
(B) 4
(C) -4
(D) + 4i
- No term in G.P is:
(A) 3
(B) 2
(C) s1
(D) 0
- -a - ib equals:
(A) a + ib
(B) -a + ib
(C) a - ib
(D) -a - ib
- w3 equals:
(A) 0
(B) -1
(C) i
(D) 1
- Sum of complex roots of unity equals:
(A) 0
(B) -1
(C) 1
(D) w
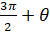 lies in:
lies in:
(A)1st quadrant
(B)2nd quadrant
(C)3rd quadrant
(D)4th quadrant
- Period of
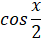 is:
is:
(A) π
(B) 2π
(C) 4π
(D) 
- With usual notations, in any triangle ABC. if Δ = 20, a = 4, b = 6, c = 10,then r equals:
(A) 2
(B) 5
(C) 10
(D) 15
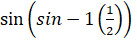 equals:
equals:
(A) 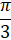
(B) 
(C) 
(D) 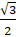
- With usual notations, r1 equals:
(A) 
(B) 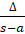
(C) 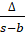
(D) 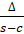
- If sin x =
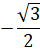 , then reference angle is:
, then reference angle is:
(A) 
(B) 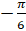
(C) 
(D) 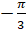
- If A and B are disjoint events, then P (AUB) equals:
(A) P(A)+P(B)
(B) P(A)+P(B)-P(A ∩ B),
(C) P(A)+P(A ∩ B)
(D) P(A) - P(B)
- If two dice are thrown simultaneously, then the number of elements in the sample space are:
(A) 6
(B) 12
(C) 24
(D) 36
- The number of terms in the expansion of (1 +x)1/2, |x| < 1 are:
(A) 2
(B) n
(C) 
(D) infinite
- If n is positive integer, then n2 > n+ 3 is true when:
(A) n >3
(B) n >2
(C) n >1
(D) n <3
- Cot² 0 - cosec² 0 equals:
(A) 1
(B) -1
(C) cot0
(D) cosec0
Rawalpindi Board 2017
INTERMEDIATE (12th CLASS)
PART-II
Mathematics
(NEW SCHEME)
TIME ALLOWED: 2.30 Hours
MAXIMUM MARKS: 80
SUBJECTIVE
SECTION-I
2. Attempt any Eight of the following. All carry equal marks.
(i) Show that ∀ z ∈ cz² + z-2 is a real number.
(ii) Simplify by justifying each step 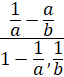
(iii) Write down the power set of {9, 11}.
(iv) Solve by using quadratic formula 15x² + 2ax — a² = 0.
(v) Convert (AUB)’ = A'UB' into logic form.
(vi) If a, b are elements of a group G, solve ax = b.
(vii) Show that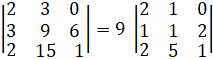
(viii) Prove that 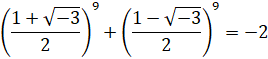
(ix) Simplify (5, —4) ÷ (-3, —8).
(x) If A =  and A² =
and A² = 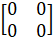 find the values of a and b.
find the values of a and b.
(xi) lf the matrices A and B are symmetric and AB = BA. Show that AB is symmetric.
(xii) Show that roots of (p + q)x² — px q = 0 are rational.
3. Attempt any eight parts.
(i) Resolve 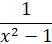 into partial fractions.
into partial fractions.
(ii) Find next two terms of sequence -1, 2, 2, 40,---------
(iii) Find A.M between x — 3 and x + 5.
(iv) Write 8.7.6.5 in the factorial form.
(v) Evaluate 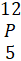
(vi) if 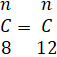 find n:
find n:
(vii) Find vulgar fraction equivalent to 0.7° recurring decimal.
(viii) If the numbers 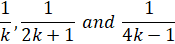 are in Harmonic sequence, find k.
are in Harmonic sequence, find k.
(ix) Determine the probability of getting 2 hands in two successive tosses of a balanced coin.
(x) Show that 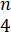 >
> 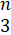 +4 is not true for n = 1.
+4 is not true for n = 1.
(xi) Calculate (2.02)4 by means of binomial theorem.
(xii) Expand (1 + 2x)-1 up to four terms.
4. Attempt any six parts.
Convert 18°6'21" to decimal form.
(ii) Prove that: cos² θ - sin² θ = cos4 θ - sin4 θ.
(iii) - Find the value of tan 105° (without calculator).
(iv) Prove that 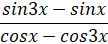 cot2x .
cot2x .
(v) Find the value of sin 105°.
(vi) Express cos(x + y) sin(x — y) as sum or difference.
(vii) Find the period of sin x/5.
(viii) State the law of cosine.
(ix) Show that: 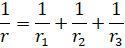 .
.
(x) Find domain and range of y = cos-1x.
(xi) Solve the equation 1+ cos x = 0.
(xii) Find the solution of sec x = -2, x ∈ [0,2π].
(xiii) Find the area of the triangle ABC in which a = 18, b = 24, c = 30.
SECTION-II
NOTE: Attempt any three questions.
5. (a) Show that 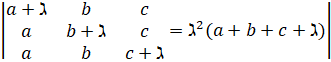
(b) If a and β are the roots of 5x² -x -2 = 0 form the equation roots are 3/a and 3/β.
6. (a) Resolve 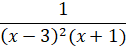 into partial fractions.
into partial fractions.
(b) lf the (Positive) G.M and H.M between two numbers are 4 and  , find the numbers.
, find the numbers.
7. (a) How many numbers greater than one million can be formed from the digits 0,2,2,2,3,4,4?
(b) Find co-efficient of the term involving x-1 in the expansion of 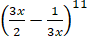
8. (a) Prove that: 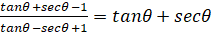 .
.
(b) Prove that: 
9. (a) Prove that in an equilateral triangle r : R : r1 = 1:2:3
(b) Prove that sin-1  sin-1
sin-1 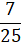 = cos-1
= cos-1 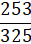
 will be of the form:
will be of the form: 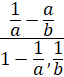
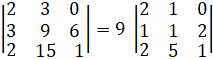
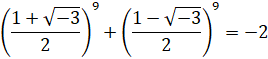
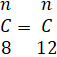 find n:
find n: