SAHIWAL Board 2017
INTERMEDIATE PART-I (11th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 20 Minutes
MAXIMUM MARKS: 15
OBJECTIVE
Note: You have four chokes for each objective type question as A, B, C and D. The choice which you think is correct; fill that circle in front of that question number. Use marker or pen to fill the circles. Cutting or filling two or more circles will result in zero mark in that question. Attempt as many questions as given in objective type question paper and leave others blank. No credit will be awarded in case BUBBLES are not filled. Do not salve question on this sheet of OBJECTIVE PAPER.
Q.No.1
- If Cos2x=0 solution in 1st quadrats is:
(A) 30°
(B) 60°
(C) 45°
(D) 15°
- Tan-1(-1) =
(A) 
(B) -
(C) 
(D) -
- In an equilateral
 ABC, r: R=
ABC, r: R=
(A) 2:3
(B) 1: 2
(C) 3: 2
(D) 2: 1
- Tan
 =
=
(A) 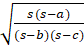
(B) 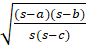
(C) 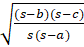
(D) 
- Domain of sin x is:
(A) {-1. 1}
(B)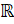
(C) 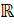 - {0}
- {0}
(D) Q
- Sin (
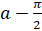 ) =
) =
(A)-Sin 
(B) Cos 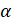
(C) Sin 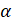
(D) -Cos 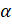
- Cos (-60°) =
(A) 
(B) -
(C) 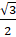
(D) -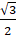
- Number of term in the expansion of
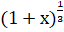 is:
is:
(A) 6
(B) 7
(C) 
(D) infinite
- Sum of coefficient in the expansion of (1 + x)n =
(A) n2
(B)2n-1
(C) 2n
(D) 2n- 1
- The value of
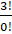 is:
is:
(A) 3
(B) 4
(C) 2
(D) 6
- An event E is said to be sure if P (A) =
(A) 0
(B) 1
(C) 
(D) 
- A.G. H. are in
(A) A.P
(B) G.P
(C) H.P
(D) Series
- The next term of 7, 9, 12…is:
(A) 16
(B) 15
(C) 14
(D) 18
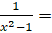
(A) 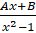
(B) 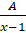
(C) 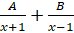
(D) 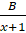
- If 4-x-
 , then x=
, then x=
(A) 1
(B) -
(C) -1
(D) =
- Sum of all the cube roots of unity is:
(A) 0
(B) 1
(C) -1
(D) -3
- If A is square matrix then (AB)t=
(A) 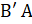
(B) 
(C) 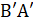
(D) AB
- If a matrix A is of order m x n then A has number of elements:
(A) m x n
(B) m + n
(C) m - n
(D) m
- The net of integers Z is a group with respect to:
(A) +
(B) x
(C) -
(D) 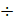
- Number
 is:
is:
(A) Rational
(B) Irrational
(C) Rime
(D) Whole
Sahiwal Board 2017
INTERMEDIATE (12th CLASS)
Mathematics (NEW SCHEME)
TIME ALLOWED: 2.30 Hours
MARKS: 80
PART-II
SUBJECTIVE
SECTION-I
2. Attempt any Eight of the following. All carry equal marks.
- Does the set {1,-1} possess closure property with respect to addition?
- Factorize 9a² + 16b²
- Show that
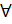 Z
Z 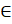 C,) z – z)2is real number
C,) z – z)2is real number
- Write down the power net of {a,{b,c}}.
- Construct truth table for (p ^
 p)
p)
- Define semi-group
- Solve the matrix equation for x
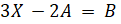 if
if 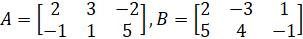
- Find x and y if
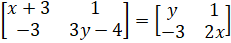
- Without expansions how that
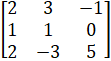 =0
=0
- Show that the roots of (p +q) x2- px -q = 0 are rational.
- Solve = x-2-10 =3x-1
- Use the factor theorem to determine x-1 is a factor of x2 +4x – 5.
3. Attempt any eight parts.
- Convert into proper form of
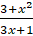
- Find a7 of 2, 6, 11, 17………..
- Find two A.Ms between 5 and 8.
- How many terms of the series -7 + (-5) + (-3)+…………….amount to 65.
- Find the 11thterm of G.P. 1+1. 2,

- Define permutation.
- Find n if
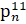 = 11 x 10 x 9.
= 11 x 10 x 9.
- Find n if
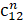 =
= .
.
- Define sample space.
- Verify
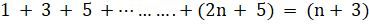 2 for n =1 and 3.
2 for n =1 and 3.
- Expand (a + 2b)3 using binomial theorem.
- Expand up to 4 terms of
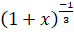
4. Attempt any six parts.
- Find
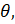 when
when 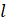 = 1.5cm, r = 2.5cm
= 1.5cm, r = 2.5cm
- Prove any one of the fundamental identities of trigonometry.
- Verify the following
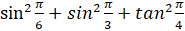 =2
=2
- State fundamental law of trigonometry.
- Prove that sin (
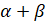 ) =
) = 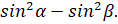
- Prove that cos (3600 -
 ) = cos
) = cos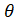 .
.
- Find the period of cot
 .
.
- State “the Law of sines”.
- By using the Law of sines show that
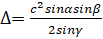
- Show that r= a sin
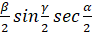 .
.
- What is the domain and range of sin x?
- (xi) Find the solutions of sin x = -
 in [0, 2
in [0, 2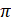 ].
].
- (xiii) Solve the trigonometric equation tan2
 =
=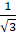 .
.
SECTION-II
NOTE: Attempt any three questions.
5. (a) Show that the set {1. } when
} when 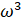 = 1 is an abelian group with respect to ordinary multiplication.
= 1 is an abelian group with respect to ordinary multiplication.
(b) Without expansion verify that 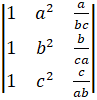 =0
=0
6. (a) If  are the roots of equation
are the roots of equation 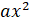 + bx +c = 0 Form the equation whose roots are (
+ bx +c = 0 Form the equation whose roots are (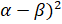 and (
and ( .
.
(b) Resolve  in partial fractions.
in partial fractions.
7. (a) Sum to n terms the series: 3+33 + 333+ .....
(b) Identify, the series: 1+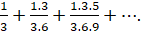 as a binomial expansion and find its sum.
as a binomial expansion and find its sum.
8. (a) Prove that 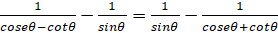
(b) Reduce cos4 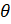 to an expression involving only function of multiples ore raised to first power.
to an expression involving only function of multiples ore raised to first power.
9. (a) Prove that 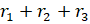 - r = 4R
- r = 4R
(b) Prove that sin-1 + sin-1
+ sin-1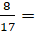 sin-1
sin-1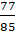
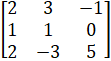 =0
=0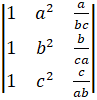 =0
=0